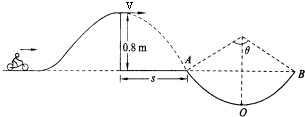
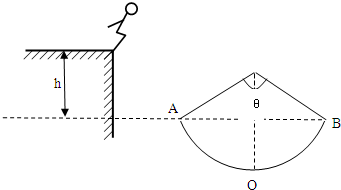如图所示，一玩滚轴溜冰的小孩（可视作质点）质量为m=30kg，他在左侧平台上滑行一段距离后平抛，恰能无碰撞地从A进入光滑竖直圆弧轨道并沿轨道下滑，A、B为圆弧两端点，其连线水平．已知圆弧半径为R=1.0m，对应圆心角为θ=106°，平台与AB连线的高度差为h=0.8m．（计算中取g=10m/s²，sin53°=0.8，cos53°=0.6）求
（1）小孩平抛的初速度大小．
（2）若小孩运动到圆弧轨道最低点O时的速度为vx=

33

m/s，则小孩对轨道的压力为多大．

如图所示，真空室内存在宽度为d=8cm的匀强磁场区域，磁感应强度B=0.332T，磁场方向垂直于纸面向里；ab、cd足够长，cd为厚度不计的金箔，金箔右侧有一匀强电场区域，电场强度E=3.32×10⁵N/C；方向与金箔成37°角．紧挨边界ab放一点状α粒子放射源S，可沿纸面向各个方向均匀放射初速率相同的α粒子，已知：α粒子的质量m=6.64×10^-27kg，电荷量q=+3.2×10^-19C，初速度
v=3.2×10⁶m/s．不计粒子重力（sin37°=0.6，cos37°=0.8）
求：（1）α粒子在磁场中作圆周运动的轨道半径R；
（2）金箔cd被α粒子射中区域的长度L；
（3）设打在金箔上d端离cd中心最远的α粒子，速度方向不变穿出金箔进入电场．在电场中运动通过N点，SN⊥ab且SN=40cm，则此α粒子从金箔上穿出时的速度大小为多少？

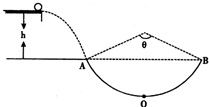如图所示，半径R=1.0m的光滑圆弧轨道固定在竖直平面内，其圆心角θ=106°，两端点A、B连线水平，质量为1㎏的小球自左侧平台上平抛后恰能无碰撞地从A点进入圆形轨道并沿轨道下滑．已知平台与AB连线高度差为h=0.8m（已知sin53°=0.8）
求：（1）小球平抛的初速度v₀；
（2）小球运动到圆弧最低点O时对轨道的压力．

如图所示，直角坐标系xOy中，M点的横坐标x_M=-

4r

3

，在-

4r

3

≤x≤0区域内，有竖直向下的匀强电场；N点的横坐标x_N=r，以N为圆心、r为半径的圆内及圆边界上有垂直于纸面向里的匀强磁场．P为磁场边界上一点．NP与竖直方向的夹角α=37°．从M点沿x轴正方向发射一质量为m、电荷量为q的带负电粒子，粒子速度大小为υ₀，粒子沿过P点的切线方向射出电场．后经P点进人磁场运动且经过N点，不计粒子重力，sin37°=0.6，cos37°=0.8．求：
（1）匀强电场的电场强度E；
（2）匀强磁场的磁感应强度B；
（3）粒子从M点到第一次经过N点所用的时间t．

如图所示，摩托车做腾跃特技表演，沿曲面冲上高0.8m顶部水平高台，接着以v=3m/s水平速度离开平台，落至地面时，恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道，并沿轨道下滑．A、B为圆弧两端点，其连线水平．已知圆弧半径为R=1.0m，人和车的总质量为180kg，特技表演的全过程中，阻力忽略不计．（计算中取g=10m/s²，sin53°=0.8，cos53°=0.6）．求：
（1）从平台飞出到A点，人和车运动的水平距离s．
（2）从平台飞出到达A点时速度及圆弧对应圆心角θ．
（3）人和车运动到达圆弧轨道A点时对轨道的压力．
（4）人和车运动到圆弧轨道最低点O速度v′=

33

m/s此时对轨道的压力．