
题目列表(包括答案和解析)
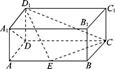
 中,
中,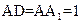 ,AB=2,点E在棱AB上移动.
,AB=2,点E在棱AB上移动.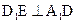 ;
;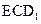 的距离;
的距离;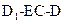 的大小为
的大小为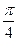 .
.(本小题满分13分)
已知,在水平平面 上有一长方体
上有一长方体 绕
绕 旋转
旋转 得到如图所示的几何体.
得到如图所示的几何体.
(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)当 时,直线
时,直线 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ,求
,求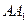 的长度;
的长度;
(Ⅲ)在(Ⅱ)条件下,设旋转过程中,平面 与平面
与平面 所成的角为
所成的角为 ,
, 长方体
长方体 的最高点离平面
的最高点离平面 的距离为
的距离为 ,请直接写出
,请直接写出 的一个表达式,并注明定义域.
的一个表达式,并注明定义域.
(本小题满分13分)
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
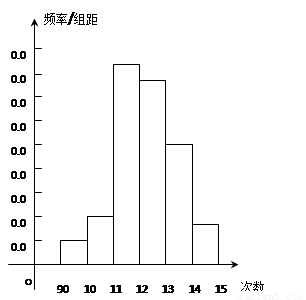
(Ⅰ)第二小组的频率是多少?样本容量是多少?
(Ⅱ)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?(Ⅲ)在这次测试中,学生跳绳次数的中位数、众数各是是多少?(精确到0.1)
(本小题满分13分)
已知,在水平平面 上有一长方体
上有一长方体 绕
绕 旋转
旋转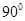 得到如图所示的几何体.
得到如图所示的几何体.

(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)当 时,直线
时,直线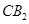 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ,求
,求 的长度;
的长度;
(Ⅲ)在(Ⅱ)条件下,设旋转过程中,平面 与平面
与平面 所成的角为
所成的角为 ,长方体
,长方体 的最高点离平面
的最高点离平面 的距离为
的距离为 ,请直接写出
,请直接写出 的一个表达式,并注明定义域.
的一个表达式,并注明定义域.
(本小题满分13分)
已知,在水平平面 上有一长方体
上有一长方体 绕
绕 旋转
旋转 得到如图所示的几何体.
得到如图所示的几何体.

(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)当 时,直线
时,直线 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ,求
,求 的长度;
的长度;
(Ⅲ)在(Ⅱ)条件下,设旋转过程中,平面 与平面
与平面 所成的角为
所成的角为 ,长方体
,长方体 的最高点离平面
的最高点离平面 的距离为
的距离为 ,请直接写出
,请直接写出 的一个表达式,并注明定义域.
的一个表达式,并注明定义域.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com