
题目列表(包括答案和解析)
(本小题满分16分)
已知椭圆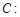
 的离心率为
的离心率为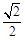 ,一条准线
,一条准线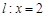 .
.
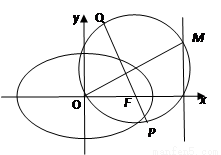
(1)求椭圆 的方程;
的方程;
(2)设O为坐标原点, 是
是 上的点,
上的点, 为椭圆
为椭圆 的右焦点,过点F作OM的垂线与以OM为直径的圆
的右焦点,过点F作OM的垂线与以OM为直径的圆 交于
交于 两点.
两点.
①若 ,求圆
,求圆 的方程;
的方程;
②若 是l上的动点,求证:点
是l上的动点,求证:点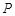 在定圆上,并求该定圆的方程.
在定圆上,并求该定圆的方程.
(本小题满分16分)
已知F是椭圆 :
: =1的右焦点,点P是椭圆
=1的右焦点,点P是椭圆 上的动点,点Q是圆
上的动点,点Q是圆 :
: +
+ =
= 上的动点.
上的动点.
(1)试判断以PF为直径的圆与圆 的位置关系;
的位置关系;
(2)在x轴上能否找到一定点M,使得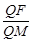 =e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
=e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
(本小题满分16分)已知椭圆 :
: 的离心率为
的离心率为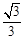 ,直线
,直线
 :
: 与椭圆
与椭圆 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左焦点为
的左焦点为 ,右焦点为
,右焦点为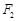 ,直线
,直线 过点
过点 且垂直与椭圆的长轴,动直线
且垂直与椭圆的长轴,动直线 垂直于直线
垂直于直线 于点
于点 ,线段
,线段 的垂直平分线交
的垂直平分线交 于点
于点 ,求点
,求点 的轨迹
的轨迹 的方程.
的方程.
(文科做)(本小题满分16分)
已知椭圆 过点
过点 ,离心率为
,离心率为 ,圆
,圆 的圆心为坐标原点,直径为椭圆的短轴,圆
的圆心为坐标原点,直径为椭圆的短轴,圆 的方程为
的方程为 .过圆
.过圆 上任一点
上任一点 作圆
作圆 的切线
的切线 ,切点为
,切点为 .
.
(1)求椭圆的方程;
(2)若直线 与圆
与圆 的另一交点为
的另一交点为 ,当弦
,当弦 最大时,求直线
最大时,求直线 的直线方程;
的直线方程;
(3)求 的最值.
的最值.
(本小题满分16分)
已知椭圆
 的离心率为
的离心率为 ,一条准线
,一条准线 .
.
(1)求椭圆 的方程;
的方程;
(2)设O为坐标原点, 是
是 上的点,
上的点, 为椭圆
为椭圆 的右焦点,过点F作OM的垂线与以OM为直径的圆
的右焦点,过点F作OM的垂线与以OM为直径的圆 交于
交于 两点.
两点.
①若 ,求圆
,求圆 的方程;
的方程;
②若 是l上的动点,求证:点
是l上的动点,求证:点 在定圆上,并求该定圆的方程.
在定圆上,并求该定圆的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com