4. m>2或m<-2 解析：因为f(x)=在（-1，1）内有零点，所以f(-1)f(1)<0,即（2+m）(2-m)<0，则m>2或m<-2

随机变量的所有等可能取值为1,2…,n，若，则（    ）

A． n=3　      　B．n=4　　        C． n=5　　      D．不能确定

5.m=-3,n=2 解析：因为的两零点分别是1与2，所以，即，解得

6．解析：因为只有一个零点，所以方程只有一个根，因此，所以

现有4个人去参加某娱乐活动，该活动有甲、乙两个游戏可供参加者选择.为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏.

（Ⅰ）求这4个人中恰有2人去参加甲游戏的概率；

（Ⅱ）求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率；

（Ⅲ）用X，Y分别表示这4个人中去参加甲、乙游戏的人数，记，求随机变量的分布列与数学期望.

【解析】依题意，这4个人中，每个人去参加甲游戏的概率为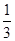，去参加乙游戏的概率为.

设“这4个人中恰有i人去参加甲游戏”为事件

则.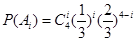

（1）这4个人中恰有2人去参加甲游戏的概率

（2）设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B，则.由于互斥，故

所以，这个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为.

（3）的所有可能取值为0,2,4.由于互斥，互斥，故

    

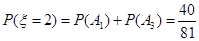
所以的分布列是

	0	2	4
P

随机变量的数学期望.

 

某校从参加高三年级理科综合物理考试的学生中随机抽出名学生，将其数学成绩（均为整数）分成六段，…后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：

（Ⅰ）求分数在内的频率，并补全这个频率分布直方图；

（Ⅱ）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的

平均分；

（Ⅲ）若从名学生中随机抽取人，抽到的学生成绩在记分，在记分，

在记分，用表示抽取结束后的总记分，求的分布列和数学期望.

【解析】（1）中利用直方图中面积和为1，可以求解得到分数在内的频率为

（2）中结合平均值可以得到平均分为：

（3）中用表示抽取结束后的总记分x, 学生成绩在的有人，在的有人，在的有人,结合古典概型的概率公式求解得到。

(Ⅰ)设分数在内的频率为，根据频率分布直方图，则有，可得，所以频率分布直方图如右图.……4分

（求解频率3分，画图1分）

（Ⅱ）平均分为：……7分

（Ⅲ）学生成绩在的有人，在的有人，

在的有人.并且的可能取值是.    ………8分

则；； ；

；.（每个1分）

所以的分布列为

	0	1	2	3	4

…………………13分