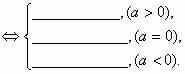
含有绝对值的不等式具有如下性质：|a|－|b|≤|a＋b|≤________．

根据此性质，可得到以下两个推论：

推论1：|a₁＋a₂＋a₃|≤________．

推论2：|a|－|b|≤|a－b|≤________．

解关于x的不等式|2x+m|<x－m(x∈R).

本题考查含有绝对值不等式的解法.解题关键是对m进行分类讨论.

含有绝对值符号的不等式，关键是去掉绝对值符号，其主要方法有：①公式法：|x|≤a(a＞0)________；|x|≥a(a＞0)________；a＜|x|＜b(0＜a＜b)________；②平方法；③零点分段讨论法．