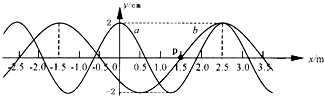
．有两列简谐横波a.b在同一媒质中沿x轴正方向传播.波速均为v＝2.5m/s.在t＝0时.两列波的波峰正好在x＝2.5m处重合.如图所示. (1)求两列波的周期Ta和Tb. (2)求t＝0时.两列——青夏教育精英家教网—

．有两列简谐横波a.b在同一媒质中沿x轴正方向传播.波速均为v＝2.5m/s.在t＝0时.两列波的波峰正好在x＝2.5m处重合.如图所示. (1)求两列波的周期Ta和Tb. (2)求t＝0时.两列波的波峰重合处的所有位置. (3)辨析题:分析并判断在t＝0时是否存在两列波的波谷重合处. 某同学分析如下:既然两列波的波峰存在重合处.那么波谷与波谷重合处也一定存在.只要找到这两列波半波长的最小公倍数.--.即可得到波谷与波谷重合处的所有位置. 你认为该同学的分析正确吗?若正确.求出这些点的位置.若不正确.指出错误处并通过计算说明理由. 解析: (1)从图中可以看出两列波的波长分别为λa＝2.5m.λb＝4.0m.因此它们的周期分别为 s＝1s s＝1.6s (2)两列波的最小公倍数为 S＝20m t＝0时.两列波的波峰生命处的所有位置为 x＝(2.520k)m.k＝0.1.2,3.-- (3)该同学的分析不正确. 要找两列波的波谷与波谷重合处.必须从波峰重合处出发.找到这两列波半波长的厅数倍恰好相等的位置.设距离x＝2.5m为L处两列波的波谷与波谷相遇.并设 L＝(2m-1) L＝(2n-1).式中m.n均为正整数只要找到相应的m.n即可将λa＝2.5m.λb＝4.0m代入并整理.得由于上式中m.n在整数范围内无解.所以不存在波谷与波谷重合处. 【查看更多】

题目列表(包括答案和解析)

有两列简谐横波a、b在同一媒质中沿x轴正方向传播，波速均为v=2.5m/s．在t=0时两列波的波峰正好在x=2.5m处重合，如图所示．

（1）求两列波的周期T_a和T_b；
（2）求t=0时两列波的波峰重合处的所有位置；
（3）辩析题：分析和判断在t=0时是否存在a列波的波谷与b列波的波峰重合处．
某同学分析如下：因为t=0时存在两列波的波峰与波峰重合处，那么a列波的波谷与b列波的波峰重合处则一定不存在．…
你认为该同学的判断正确吗？若正确，说明理由（可通过计算加以说明了）；若不正确，通过计算找出存在的重合处位置．

查看答案和解析>>