练习册

  • 练习册
  • 试题
    连续:如果函数f(x)在x=x0处有定义.且f(x)存在.并且f(x)=f(x0).则称f(x)在x=x0处连续. 【查看更多】

     

    题目列表(包括答案和解析)

    如果函数f(x)在［a,b］上连续,且在(a,b)内可导,那么如何来求f(x)在［a,b］上的最大值和最小值?

    查看答案和解析>>

    如果函数f(x)在区间[a，b]上连续，用分点a＝x0＜x1＜…＜xi－1＜xi＜…＜xn＝b，将区间[a，b]均分成n个小区间，在每个小区间[xi－1，xi]上任取一点ξi(i＝1，2，…，n)，作和式，当n→∞时，上述和式无限接近某个常数，这个常数叫做函数f(x)在区间[a，b]上的________，记作．这里a与b分别叫做积分________与积分________，区间[a，b]叫做积分________，函数f(x)叫做________，x叫做________，f(x)dx叫做________．

    查看答案和解析>>

    如果函数f(x)在区间[a，b]上连续，用分点a＝x0＜x1＜…＜xi－1＜xi＜…＜xn＝b，将区间[a，b]均分成n个小区间，在每个小区间[xi－1，xi]上任取一点ξi(i＝1，2，…，n)，作和式，当n→∞时，上述和式无限接近某个常数，这个常数叫做函数f(x)在区间[a，b]上的_________(definite integral)，记作．这里a与b分别叫做积分_________与积分_________，区间[a，b]叫做积分_________，函数f(x)叫做_________，x叫做_________，f(x)dx叫做_________．

    查看答案和解析>>

    如果函数f（x）同时满足下列条件：①在闭区间[a，b]内连续，②在开区间（a，b）内可导且其导函数为f′（x），那么在区间（a，b）内至少存在一点ξ（a＜ξ＜b），使得f（b）-f（a）=f′（ξ）（b-a）成立，我们把这一规律称为函数f（x）在区间（a，b）内具有“Lg”性质，并把其中的ξ称为中值．有下列命题：
    ①若函数f（x）在（a，b）具有“Lg”性质，ξ为中值，点A（a，f（a）），B（b，f（b）），则直线AB的斜率为f′（ξ）；
    ②函数y=
    		2-
    x2
    2
    在（0，2）内具有“Lg”性质，且中值ξ=
    		2
    ，f′（ξ）=-
    		2
    2
    ；
    ③函数f（x）=x3在（-1，2）内具有“Lg”性质，但中值ξ不唯一；
    ④若定义在[a，b]内的连续函数f（x）对任意的x1、x2∈[a，b]，x1＜x2，有
    1
    2
    [f（x1）+f（x2）]＜f（
    x1+x2
    2
    ）恒成立，则函数f（x）在（a，b）内具有“Lg”性质，且必有中值ξ=
    x1+x2
    2
    ．
    其中你认为正确的所有命题序号是
     
    ．

    查看答案和解析>>

    如果以数列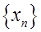的任意连续三项作边长，都能构成一个三角形，那么称这样的数列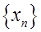为“三角形”数列；又对于“三角形”数列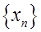，如果函数y=f(x)使得由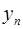=f(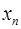)()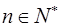确定的数列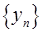仍成为一个“三角形”数列，就称y=f(x) 是数列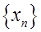的“保三角形”函数。

    （Ⅰ）、已知数列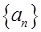是首项为2012，公比为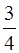的等比数列，求证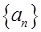：是“三角形”数列；

    （Ⅱ）、已知数列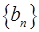是首项为2，公差为1的等差数列，若函数f(x)=  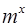(m＞0且m≠1)是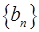的“保三角形”函数. 求m的取值范围.

     

    查看答案和解析>>


    同步练习册答案