练习册

  • 练习册
  • 试题
    在一些物理问题中.一个过程的发展.一个状态的确定.往往是由多个因素决定的.在这一决定中.若某些因素所起的作用和另一些因素所起的作用相同.则前一些因素与后一些因素是等效的.它们便可以互相代替.而对过程的发展或状态的确定.最后结果并不影响.这种以等效为前提而使某些因素互相代替来研究问题的方法就是等效法. 等效思维的实质是在效果相同的情况下.将较为复杂的实际问题变换为简单的熟悉问题.以便突出主要因素.抓住它的本质.找出其中规律.因此应用等效法时往往是用较简单的因素代替较复杂的因素.以使问题得到简化而便于求解. 赛题精讲 例1:如图4-1所示.水平面上.有两个竖直的光滑 墙壁A和B.相距为d.一个小球以初速度v0从两墙 之间的O点斜向上抛出.与A和B各发生一次弹性 碰撞后.正好落回抛出点.求小球的抛射角θ. 解析:将弹性小球在两墙之间的反弹运动.可等效为 一个完整的斜抛运动.所以可用解斜抛运动的 方法求解. 由题意得: 可解得抛射角 例2:质点由A向B做直线运动.A.B间的距离为L.已知质点在A点的速度为v0.加速度为a.如果将L分成相等的n段.质点每通过L/n的距离加速度均增加a/n.求质点到达B时的速度. 解析 从A到B的整个运动过程中.由于加速度均匀增加.故此运动是非匀变速直线运动.而非匀变速直线运动.不能用匀变速直线运动公式求解.但若能将此运动用匀变速直线运动等效代替.则此运动就可以求解. 因加速度随通过的距离均匀增加.则此运动中的平均加速度为 由匀变速运动的导出公式得 解得 例3一只老鼠从老鼠洞沿直线爬出.已知爬出速度的大小与距老鼠洞中心的距离s成反比.当老鼠到达距老鼠洞中心距离s1=1m的A点时.速度大小为.问当老鼠到达距老鼠洞中心s2=2m的B点时.其速度大小老鼠从A点到达B点所用的时间t=? 解析 我们知道当汽车以恒定功率行驶时.其速度v与牵引力F成反比.即.v=P/F.由此可把老鼠的运动等效为在外力以恒定的功率牵引下的弹簧的运动. 由此分析.可写出 当 将其代入上式求解.得 所以老鼠到达B点时的速度 再根据外力做的功等于此等效弹簧弹性势能的增加. 代入有关量可得 由此可解得 此题也可以用图像法.类比法求解. 例4 如图4-2所示.半径为r的铅球内有一半径为的 球形空腔.其表面与球面相切.铅球的质量为M.在铅球和空腔 的中心连线上.距离铅球中心L处有一质量为m的小球.求铅球对小球的引力. 解析 因为铅球内部有一空腔.不能把它等效成位于球心的质点. 我们设想在铅球的空腔内填充一个密度与铅球相同的小铅球△M.然后在对于小球m对称的另一侧位置放另一个相同的小铅球△M.这样加入的两个小铅球对小球m的引力可以抵消.就这样将空腔铅球变成实心铅球.而结果是等效的. 带空腔的铅球对m的引力等效于实心铅球与另一侧△M对m的引力之和. 设空腔铅球对m的引力为F.实心铅球与△M对m的引力分别为F1.F2. 则 F=F1-F2 ① 经计算可知:.所以 ② ③ 将②.③代入①式.解得空腔铅球对小球的引力为 例5 如图4-3所示.小球长为L的光滑斜面顶端自由下滑. 滑到底端时与挡板碰撞并反向弹回.若每次与挡板碰撞后的速度大小为碰撞前速度大小的.求小球从开始下滑到最终停止于斜面下端时.小球总共通过的路程. 解析 小球与挡板碰撞后的速度小于碰撞前的速度.说明碰撞过程中损失能量.每次反弹距离都不及上次大.小球一步一步接近挡板.最终停在挡板处. 我们可以分别计算每次碰撞垢上升的距离L1.L2.--.Ln.则小球总共通过的路程为.然后用等比数列求和公式求出结果.但是这种解法很麻烦. 我们假设小球与挡板碰撞不损失能量.其原来损失的能量看做小球运动过程中克服阻力做功而消耗掉.最终结果是相同的.而阻力在整个运动过程中都有.就可以利用摩擦力做功求出路程. 设第一次碰撞前后小球的速度分别为..碰撞后反弹的距离为L1.则 其中 碰撞中损失的动能为 根据等效性有 解得等效摩擦力 通过这个结果可以看出等效摩擦力与下滑的长度无关.所以在以后的运动过程中.等效摩擦力都相同. 以整个运动为研究过程.有 解出小球总共通过的总路程为 此题也可以通过递推法求解.读者可试试. 例6 如图4-4所示.用两根等长的轻质细线悬挂一个小球. 设L和已知.当小球垂直于纸面做简谐运动时.其周期为 . 解析 此题是一个双线摆.而我们知道单摆的周期.若将又线摆摆长等效为单摆摆长.则双线摆的周期就可以求出来了. 将双线摆摆长等效为单摆摆长.则此双线摆的周期为 例8 如图4-5所示.由一根长为L的刚性轻杆和杆端的小球组成的单摆做振幅很小的自由振动. 如果杆上的中点固定另一个相同的小球.使单摆变成一个异形复摆.求该复摆的振动周期. 解析 复摆这一物理模型属于大学普通物理学的内容.中学阶段限于知识的局限.不能直接求解. 如能进行等效操作.将其转化成中学生熟悉的单摆模型.则求解周期将变得简捷易行. 设想有一摆长为L0的辅助单摆.与原复摆等周期.两摆分别从摆角处从静止开始摆动.摆动到与竖直方向夹角为时.具有相同的角速度.对两摆分别应用机械能守恒定律.于是得 对单摆.得 联立两式求解.得 故原复摆的周期为 例9 粗细均匀的U形管内装有某种液体.开始静止在水平 面上.如图4-6所示.已知:L=10cm.当此U形管以4m/s2的 加速度水平向右运动时.求两竖直管内液面的高度差.(g=10m/s2) 解析 当U形管向右加速运动时.可把液体当做放在等效重 力场中.的方向是等效重力场的竖直方向.这时两边的液面应与等效重力场的水平方向平行.即与方向垂直. 设的方向与g的方向之间夹角为.则 由图4-6可知液面与水平方向的夹角为. 所以. 例10 光滑绝缘的圆形轨道竖直放置.半径为R.在其最低点A处放一质量为m的带电小球.整个空间存在匀强电场.使小球受到电场力的大小为.方向水平向右.现给小球一个水平向右的初速度.使小球沿轨道向上运动.若小球刚好能做完整的圆周运动.求. 解析 小球同时受到重力和电场力作用.这时也可以认为小球处在等效重力场中. 小球受到的等效重力为 等效重力加速度 与竖直方向的夹角.如图4-7甲所示.所以B点为等效重力场中轨道的最高点.如图4-7.由题意.小球刚好能做完整的圆周运动.小球运动到B点时的速度 在等效重力场中应用机械能守恒定律 将.分别代入上式.解得给小球的初速度为 例11 空间某一体积为V的区域内的平均电场强度(E)的定义为 如图4-8所示.今有一半径为a原来不带电的金属球.现 使它处于电量为q的点电荷的电场中.点电荷位于金属球外. 与球心的距离为R.试计算金属球表面的感应电荷所产生的电 场在此球内的平均电场强度. 解析 金属球表面的感应电荷产生的球内电场.由静电平衡知识可知等于电量为q的点电荷在金属球内产生的电场.其大小相等.方向相反.因此求金属球表面的感应电荷产生的电场.相当于求点电荷q在金属球内产生的电场. 由平均电场强度公式得 设金属球均匀带电.带电量为q.其密度为.则有 为带电球体在q所在点产生的场强.因而有.方向从O指向q. 例11 质量为m的小球带电量为Q.在场强为E的水平匀强电场中获得竖直向上的初速度为. 若忽略空气阻力和重力加速度g随高度的变化.求小球在运动过程中的最小速度. 解析 若把电场力Eq和重力mg合成一个力.则小球相当于只受一个力的作用.由于小球运动的初速度与其所受的合外力之间成一钝角.因此可以把小球的运动看成在等效重力作用下的斜抛运动.而做斜抛运动的物体在其速度方向与垂直时的速度为最小.也就是斜抛运动的最高点.由此可见用这种等效法可以较快求得结果. 电场力和重力的合力方向如图4-9所示. 由图所示的几何关系可知 小球从O点抛出时.在y方向上做匀减速直线运动.在x轴方向上做匀速直线运动. 当在y轴方向上的速度为零时.小球只具有x轴方向上的速度.此时小球的速度为最小值.所以 此题也可以用矢量三角形求极值的方法求解.读者可自行解决. 例12 如图4-10所示.R1.R2.R3为定值电阻.但阻值未 知.Rx为电阻箱.当Rx为时.通过它的电流 时.通过它的电流 则当时.求电阻 解析 电源电动势.内电阻r.电阻R1.R2.R3均未知. 按题目给的电路模型列式求解.显然方程数少于未知量数.于 是可采取变换电路结构的方法. 将图4-10所示的虚线框内电路看成新的电源.则等效电 路如图4-10甲所示.电源的电动势为.内电阻为. 根据 电学知识.新电路不改变Rx和Ix的对应关系.有 ① ② ③ 由①.②两式.得. 代入③式.可得 例13 如图4-11所示的甲.乙两个电阻电路具有这样的特性:对于任意阻值的RAB.RBC和RCA.相应的电阻Ra.Rb和Rc可确定. 因此在对应点A和a.B和b.C和c的电位是相同的.并且.流入对应点(例如A和a)的电流也相同.利用这些条件 证明:.并证明对Rb和Rc也有类似的结果.利用上面的结果求图4-11甲中P和Q两点之间的电阻. 解析 图4-11中甲.乙两种电路的接法分别叫三角形接法和星形接法.只有这两种电路任意两对应点之间的总电阻部分都相等.两个电路可以互相等效.对应点A.a.B.b和C.c将具有相同的电势. 由Rab=RAB.Rac=RAC.Rbc=RBC.对ab间.有 ① 同样.ac间和bc间.也有 ② ③ 将①+②-③得: 再通过①-②+③和③+②-①.并整理.就得到Rb和RC的表达式. 下面利用以上结果求图4-12乙中P和Q两点之间的电阻. 用星形接法代替三角形接法.可得图4-12乙所示电路.PRQS回路是一个平衡的惠斯登电桥.所以在RS之间无电流.因此它与图4-12丙所示电路是等效的. 因此PQ之间的总电阻RPQ可通过这三个并联电阻求和得到. 例14 如图4-13所示.放在磁感应强度B=0.6T的匀强磁场中的长方形金属线框abcd.框平面与磁感应强度方向垂直.其中ab和bc各是一段粗细均匀的电阻丝Rab=5Ω.Rbc=3Ω.线框其余部分电阻忽略不计.现让导体EF搁置在ab.cd边上.其有效长度L=0.5m.且与ab垂直.阻值REF=1Ω.并使其从金属框ad端以恒定的速度V=10m/s向右滑动.当EF滑过ab长的4/5距离时.问流过aE端的电流多大? 解析 EF向右运动时.产生感应电动势.当EF滑过ab长的时.电路图可等效为如图4-13甲所示的电路. 根据题设可以求出EF产生的感应电动势. 此时电源内阻为导体EF的电阻..则电路中的总电阻为 电路中的总电流为 ∴通过aE的电流为 例15 有一薄平凹透镜.凹面半径为0.5m.玻璃的折射 率为1.5.且在平面上镀一层反射层.如图4-14所示.在此 系统的左侧主轴上放一物S.S距系统1.5m.问S成像于何处? 解析 本题可等效为物点S先经薄平凹透镜成像.其像为 平面镜的物.平面镜对物成像又为薄平凹透镜成像的物.根据 成像规律.逐次求出最终像的位置. 根据以上分析.首先考虑物S经平凹透镜的成像. 根据公式 其中 故有 成像在左侧.为虚像.该虚像再经平凹透镜成像后.其像距为 成像在右侧.为虚像.该虚像再经平凹透镜成像.有 故成虚像于系统右侧0.375m处 此题还可用假设法求解. 【查看更多】

     

    题目列表(包括答案和解析)

    ［物理——选修3-3］（15分）

       （1）（5分）在研究性学习的过程中，针对能源危机、大气污染等问题同学们提出如下四个活动方案，哪些从理论上讲是可行的                                             

    A．某国际科研小组正在研制利用超导材料制成灯泡的灯丝和闭合电路，利用电磁感应激起电流后，由于电路电阻为零从而使灯泡一直发光

    B．发明一种制冷设备，使温度降至绝对零度以下

    C．汽车尾气中各类有害气体排入大气后严重污染了空气，想办法使它们自发地分离，既清洁了空气，又变废为宝，成为新能源

    D．将房屋顶盖上太阳能板，可直接用太阳能来解决照明和热水问题

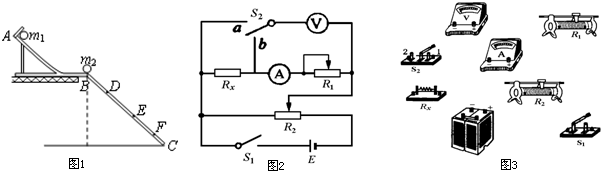
       （2）（10分）如图所示，用面积为S的活塞在汽缸内封闭着一定质量的空气，活塞上放一砝码，活塞和砝码的总质量为m，现对汽缸缓缓加热使汽缸内的空气温度从T1升高到T2，且空气柱的高度增加了∆l， 已知加热时气体吸收的热量为Q，外界大气压强为P0，问：此过程中被封闭气体的内能变化了多少？

     

     

     

     

     

     

     

     

     

    查看答案和解析>>

    在超低温条件下，物质的许多性质会发生意想不到的变化．荷兰科学家卡末林·昂内斯1908年首次将氦液化，获得了1.5K左右的低温，并于1911年通过实验发现了在4.2K左右汞的超导导电状态，因此获得了1913年诺贝尔物理学奖．爱因斯坦曾预言，如果将某些特定原子气体冷却到非常低的温度，那么所有原子会突然以可能的最低能态凝聚，其过程就像在气体中形成液滴，这就是著名的“玻色－爱因斯坦凝聚”．1995年，美国科学家康奈尔和维曼终于在比绝对零度高出千万分之二度的超低温度下，使约2000个铷原子形成了“玻色－爱因斯坦凝聚”，同时德国科学家克特勒独立地用钠原子进行实验，也获得了同样的成功．因此，这三位科学家共同获得2001年诺贝尔物理学奖．

    请仔细阅读以上文字，并回答下列问题：

    (1)超导材料电阻降为零的温度称为临界温度，1987年我国科学家制成临界温度为90K的高温超导体，其临界温度对应的摄氏温度为多少？

    (2)利用超导材料零电阻的性质，可实现无损耗输电．现有一直流电路，输电线的总电阻为0.4Ω，它提供给用电器的电功率为40kW，电压为800V．如果用临界温度以下的超导电缆替代原来的输电线，保持供给用电器的功率和电压不变，那么节约的电功率为多少？

    查看答案和解析>>

    （2009?湘潭模拟）（1）为了验证碰撞中的动量守恒，某同学选取了两个体积相同、质量不相等的小球，按下述步骤做了如下实验：

    A．用天平测出两个小球的质量（分别为m1和m2，且m1＞m2）．
    B．按照如图1所示的那样，安装好实验装置．将斜槽AB固定在桌边，使槽的末端点的切线水平．将一斜面BC连接在斜槽末端．
    C．先不放小球m2，让小球m1从斜槽顶端A处由静止开始滚下，记下小球在斜面上的落点位置．
    D．将小球m2放在斜槽前端边缘处，让小球m1从斜槽顶端A处滚下，使它们发生碰撞，记下小球m1和小球m2在斜面上的落点位置．
    E．用毫米刻度尺量出各个落点位置到斜槽末端点B的距离．图1中D、E、F点是该同学记下的小球在斜面上的几个落点位置，到B点的距离分别为LD、LE、LF．
    根据该同学的实验，回答下列问题：
    ①小球m1与m2发生碰撞后，m1的落点是图1中的
    D
    D
    点，m2的落点是图中的
    F
    F
    点．
    ②用测得的物理量来表示，只要满足关系式
    m1
    		LE
    =m1
    		LD
    +m2
    		LF
    m1
    		LE
    =m1
    		LD
    +m2
    		LF
    ，则说明碰撞中动量是守恒的．
    （2）用伏安法测电阻时，由于电压表、电流表内阻的影响，不论使用电流表内接法还是电流表外接法，都会产生系统误差．为了消除系统误差，某研究性学习小组设计了如图2所示的测量电路．
    ①请完成下列操作过程：
    第一步：先将R2的滑动头调到最左端，单刀双掷开关S2合向a，然后闭合电键S1，调节滑动变阻器R1和R2，使电压表和电流表的示数尽量大些（不超过量程），读出此时电压表和电流表的示数U1、I1．
    第二步：保持两滑动变阻器的滑动触头位置不变，
    将单刀双掷开关S2合向b，读出此时电压表和电流表的示数U2、I2．
    将单刀双掷开关S2合向b，读出此时电压表和电流表的示数U2、I2．
    ．
    ②根据以上记录数据写出被测电阻Rx的表达式Rx=
    U1
    I1
    -
    U2
    I2
    U1
    I1
    -
    U2
    I2
    ．
    ③根据实验原理图3连接好实物图．

    查看答案和解析>>

    实验题：

    （1）几位同学做“用插针法测定玻璃的折射率”实验，图示直线aa′、bb′表示在白纸上画出的玻璃的两个界面．几位同学进行了如下操作：
    A．甲同学选定的玻璃两个光学面aa′、bb′不平行，其它操作正确．
    B．乙同学在白纸上正确画出平行玻璃砖的两个界aa′、bb′后，将玻璃砖向aa′方向平移了少许，其它操作正确．
    C．丙同学在白纸上画aa′、bb′界面时，其间距比平行玻璃砖两光学界面的间距稍微宽些，其它操作正确．
    上述几位同学的操作，对玻璃折射率的测定结果没有影响的是
    AB
    AB
    （填写字母代号）
    （2）实验桌上有下列实验仪器：
    A．待测电源（电动势约3V，内阻约7Ω）；
    B．直流电流表（量程0～0.6～3A，0.6A档的内阻约0.5Ω，3A档的内阻约0.1Ω；）
    C．直流电压表（量程0～3～15V，3V档内阻约5kΩ，15V档内阻约25kΩ）；
    D．滑动变阻器（阻值范围为0～15Ω，允许最大电流为1A）；
    E．滑动变阻器（阻值范围为0～1000Ω，允许最大电流为0.2A）；
    F．开关、导线若干；
    G．小灯泡“4V、0.4A”．
    请你解答下列问题：
    ①利用给出的器材测量电源的电动势和内阻，要求测量有尽可能高的精度且便于调节，应选择的滑动变阻器是
    D
    D
    （填代号），理由是
    由于电源内阻较小，选择全电阻较小的滑动变阻器D便于调节，能使电表示数发生明显变化．
    由于电源内阻较小，选择全电阻较小的滑动变阻器D便于调节，能使电表示数发生明显变化．
    ；
    ②请将图甲中实物连接成实验电路图；
    ③某同学根据测得的数据，作出U-I图象如图乙中图线a所示，由此可知电源的电动势E=
    3.0
    3.0
    V，内阻r=
    7.5
    7.5
    Ω；
    ④若要利用给出的器材通过实验描绘出小灯泡的伏安特性曲线，要求测量多组实验数据，请你在虚线框内画出实验原理电路图；
    ⑤将④步中得到的数据在同一U-I坐标系内描点作图，得到如图乙所示的图线b，如果将此小灯泡与上述电源组成闭合回路，此时小灯泡的实际功率为
    0.30
    0.30
    W．

    查看答案和解析>>


    同步练习册答案