
题目列表(包括答案和解析)
![]()
图1
A.左方是A球,碰撞后A、B两球速度大小之比为2∶5?
B.左方是A球,碰撞后A、B两球速度大小之比为1∶10?
C.右方是A球,碰撞后A、B两球速度大小之比为2∶5?
D.右方是A球,碰撞后A、B两球速度大小之比为1∶10?
如图17所示,光滑水平面上有大小相同的A、B两球在同一直线上运动,两球质量关系为mB=2mA,规定向右为正方向,A、B两球的动量均为6 kg·m·s-1,运动中两球发生碰撞,碰撞后A球的动量增量为-4 kg·m·s-1,则( )
![]()
图17
A.左方是A球,碰撞后A、B两球速度大小之比为2∶5
B.左方是A球,碰撞后A、B两球速度大小之比为1∶10
C.右方是A球,碰撞后A、B两球速度大小之比为2∶5
D.右方是A球,碰撞后A、B两球速度大小之比为1∶10
如图 6 所示,光滑水平面上有大小相同的 A 、B 两球在同一直线上运动,两球质量关系为 mB = 2mA,规定向右为正方向,A 、B 两球的动量均为 6kg·m/s,运动中两球发生碰撞,碰撞后 A 球的动量增量为 -4kg·m/s,则( )
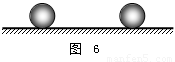
A.左方是 A 球,碰撞后 A 、B 两球速度大小之比为 2∶5
B.左方是 A 球,碰撞后 A 、B 两球速度大小之比为 1∶10
C.右方是 A 球,碰撞后 A 、B 两球速度大小之比为 2∶5
D.右方是 A 球,碰撞后 A 、B 两球速度大小之比为 1∶10
如图 6 所示,光滑水平面上有大小相同的 A 、B 两球在同一直线上运动,两球质量关系为 mB = 2mA,规定向右为正方向,A 、B 两球的动量均为 6kg·m/s,运动中两球发生碰撞,碰撞后 A 球的动量增量为 -4kg·m/s,则( )

A.左方是 A 球,碰撞后 A 、B 两球速度大小之比为 2∶5
B.左方是 A 球,碰撞后 A 、B 两球速度大小之比为 1∶10
C.右方是 A 球,碰撞后 A 、B 两球速度大小之比为 2∶5
D.右方是 A 球,碰撞后 A 、B 两球速度大小之比为 1∶10
如图10所示,光滑水平面上有一长板车,车的上表面OA段是一长为L的水平粗糙轨道,A的右侧光滑,水平轨道左侧是一光滑斜面轨道,斜面轨道与水平轨道在O点平滑连接.车右端固定一个处于锁定状态的压缩轻弹簧,其弹性势能为Ep,一质量为m的小物体(可视为质点)紧靠弹簧,小物体与粗糙水平轨道间的动摩擦因数为μ,整个装置处于静止状态.现将轻弹簧解除锁定,小物体被弹出后滑上水平粗糙轨道.车的质量为 2m,斜面轨道的长度足够长,忽略小物体运动经过O点处产生的机械能损失,不计空气阻力.求:
(1)解除锁定结束后小物体获得的最大动能;
(2)当μ满足什么条件小物体能滑到斜面轨道上,满足此条件时小物体能上升的最大高度为多少?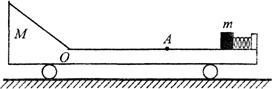
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com