
题目列表(包括答案和解析)
(本小题满分12分)二次函数![]() 的图象经过三点
的图象经过三点![]() .
.![]()
(1)求函数![]() 的解析式(2)求函数
的解析式(2)求函数![]() 在区间
在区间![]() 上的最大值和最小值
上的最大值和最小值
(本小题满分12分)已知等比数列{an}中,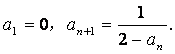
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设数列{an}的前n项和为Sn,证明:![]() ;
;
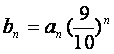 ,证明:对任意的正整数n、m,均有
,证明:对任意的正整数n、m,均有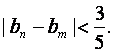
(本小题满分12分)已知函数![]() ,其中a为常数.
,其中a为常数.
(Ⅰ)若当![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
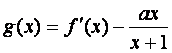 的单调区间.
的单调区间.(本小题满分12分)
甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为![]() ,乙投篮命中的概率为
,乙投篮命中的概率为![]()
(Ⅰ)求甲至多命中2个且乙至少命中2个的概率;
(Ⅱ)若规定每投篮一次命中得3分,未命中得-1分,求乙所得分数η的概率分布和数学期望.(本小题满分12分)已知![]() 是椭圆
是椭圆![]() 的两个焦点,O为坐标原点,点
的两个焦点,O为坐标原点,点![]() 在椭圆上,且
在椭圆上,且![]() ,圆O是以
,圆O是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与圆O相切,并且与椭圆交于不同的两点A、B.
与圆O相切,并且与椭圆交于不同的两点A、B.
(1)求椭圆的标准方程;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)当![]() 时,求弦长|AB|的取值范围.
时,求弦长|AB|的取值范围.
1.B 2.D 3.A 4.A 5.A 6.B 7.B 8.B 9.C 10.C
11. 12.4 13.2.442 14.
12.4 13.2.442 14. 15.9,15
15.9,15
16.(Ⅰ) ,∴
,∴ ,
,
∴ ,∴
,∴
 (Ⅱ)
(Ⅱ)


 ,∴
,∴ ,
,
∴
17.(Ⅰ)从4名运动员中任取两名,其靶位号与参赛号相同,有 种方法,另2名运动员靶位号与参赛号均不相同的方法有1种,所以恰有一名运动员所抽靶位号与参赛号相同的概率为
种方法,另2名运动员靶位号与参赛号均不相同的方法有1种,所以恰有一名运动员所抽靶位号与参赛号相同的概率为 
(Ⅱ)①由表可知,两人各射击一次,都未击中9环的概率为P=(1-0.3)(1-0.32)=0.476 至少有一人命中9环的概率为p=1-0.476=0.524
至少有一人命中9环的概率为p=1-0.476=0.524
②

所以2号射箭运动员的射箭水平高.
18.(Ⅰ)设椭圆方程为 ,则有
,则有 ,∴a=6, b=3.∴椭圆C的方程为
,∴a=6, b=3.∴椭圆C的方程为
(Ⅱ) ,设点
,设点 ,则
,则
 ∴
∴ ,∵
,∵ ,∴
,∴ ,∴
,∴ ∴
∴ 的最小值为6.
的最小值为6.
19.(Ⅰ)在梯形ABCD中,∵ ,
,
∴四边形ABCD是等腰梯形,
且
∴ ,∴
,∴
 又∵平面
又∵平面 平面ABCD,交线为AC,∴
平面ABCD,交线为AC,∴ 平面ACFE.
平面ACFE.
(Ⅱ)当 时,
时, 平面BDF. 在梯形ABCD中,设
平面BDF. 在梯形ABCD中,设 ,连结FN,则
,连结FN,则
∵ 而
而 ,∴
,∴ ∴MF
∴MF AN,
AN,
∴四边形ANFM是平行四边形. ∴
又∵ 平面BDF,
平面BDF, 平面BDF. ∴
平面BDF. ∴ 平面BDF.
平面BDF.
(Ⅲ)取EF中点G,EB中点H,连结DG、GH、DH,∵DE=DF,∴ ∵
∵ 平面ACFE,∴
平面ACFE,∴ 又∵
又∵ ,∴
,∴ 又∵
又∵ ,∴
,∴
∴ 是二面角B―EF―D的平面角.
是二面角B―EF―D的平面角.
在△BDE中 ∴
∴ ∴
∴ ,
,

 ∴
∴ 又
又 ∴在△DGH中,
∴在△DGH中,
由余弦定理得 即二面角B―EF―D的大小为
即二面角B―EF―D的大小为
20.(Ⅰ)设 ,
, ,
,
∴ 在
在 单调递增.
单调递增.
(Ⅱ)当 时,
时, ,又
,又 ,
,
 ,即
,即 ;
;
当 时,
时, ,
,
 ,由
,由 ,得
,得 或
或 .
.
 的值域为
的值域为
 (Ⅲ)当x=0时,
(Ⅲ)当x=0时, ,∴x=0为方程的解.
,∴x=0为方程的解.
当x>0时, ,∴
,∴ ,∴
,∴
当x<0时, ,∴
,∴ ,∴
,∴
即看函数
与函数 图象有两个交点时k的取值范围,应用导数画出
图象有两个交点时k的取值范围,应用导数画出 的大致图象,
的大致图象,
∴ ,∴
,∴
21.(Ⅰ)当 时,
时,
 ,∴
,∴ ,令
,令 有x=0,
有x=0,
当 单调递减;当
单调递减;当 单调递增.
单调递增.
∴ ∴
∴ ;
;
(Ⅱ)∵ ,∴
,∴ ∴
∴
∴ 为首项是1、公比为
为首项是1、公比为 的等比数列. ∴
的等比数列. ∴ ∴
∴ ;
;
(Ⅲ)∵ ,由(1)知
,由(1)知 ,
,
∴ ,即证.
,即证.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com