练习册

  • 练习册
  • 试题
    如图.为坐标原点.A.B是单位圆O上的动点.C是圆与x轴正半轴的交点.设． (Ⅰ)当点A的坐标为时.求的值,(Ⅱ)若.且当点A.B在圆上沿逆时针方向移动时.总有.试求BC的取值范围． 考点突破专题十七 常见的数学思想方法(2) 039轨迹方程 [自我提醒] 【查看更多】

     

    题目列表(包括答案和解析)

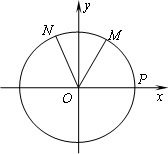
    如图，设P是单位圆和x轴正半轴的交点，M、N是单位圆上的两点，O是坐标原点，，∠PON＝α，，，则f(α)的范围为

    [　　]
    A．

    ．

    B．

    C．

    ．

    D．

    ．

    查看答案和解析>>

    [选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．
    A．（选修4-1：几何证明选讲）
    如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，求线段AE的长．
    B．（选修4-2：矩阵与变换）
    已知二阶矩阵A有特征值λ1=3及其对应的一个特征向量α1=
    1
    1
    ，特征值λ2=-1及其对应的一个特征向量α2=
    1
    -1
    ，求矩阵A的逆矩阵A-1．
    C．（选修4-4：坐标系与参数方程）
    以平面直角坐标系的原点O为极点，x轴的正半轴为极轴，建立极坐标系（两种坐标系中取相同的单位长度），已知点A的直角坐标为（-2，6），点B的极坐标为(4，
    π
    2
    )    ，直线l过点A且倾斜角为
    π
    4
    ，圆C以点B为圆心，4为半径，试求直线l的参数方程和圆C的极坐标方程．
    D．（选修4-5：不等式选讲）
    设a，b，c，d都是正数，且x=
    		a2+b2
    ，y=
    		c2+d2
    ．求证：xy≥
    		(ac+bd)(ad+bc)
    ．

    查看答案和解析>>

     【选做题】本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．

    A.选修4-1：几何证明选讲

     

    如图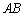，是⊙O的直径，弦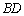、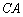的延长线相交于点E，EF垂直BA的延长线于点F．求证：

    （1）；

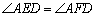    （2）．

     

     

     

     

     

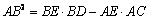    B.选修4-2：矩阵与变换

     

    求曲线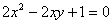在矩阵MN对应的变换作用下得到的曲线方程，其中，．

     

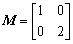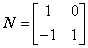    C.选修4-4：坐标系与参数方程

     

    以直角坐标系的原点为极点，x轴的正半轴为极轴，并在两种坐标系中取相同的单位长度.已知直线l的极坐标方程为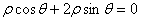，曲线C的参数方程为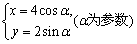，又直线l与曲线C交于A，B两点，求线段AB的长.

     

    D.选修4-5：不等式选讲

     

    若存在实数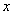使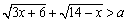成立，求常数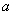的取值范围．

     

     

    查看答案和解析>>

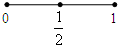    精英家教网以下是面点师一个工作环节的数学模型：如图，在数轴上截取与闭区间[0，1]对应的线段，对折后（坐标1所对应的点与原点重合）再均匀的拉成一个单位长度的线段，这一过程称为一次操作（例如在第一次操作完成后，原来的坐标
    1
    4
    ，
    3
    4
    变成
    1
    2
    ，原来的坐标
    1
    2
    变成1，等等）．则区间[0，1]上（除两个端点外）的点，在第二次操作完成后，恰好被拉到与1重合的点所对应的坐标是
    1
    4
    ，
    3
    4
    ，那么在第n次操作完成后（n≥1），恰好被拉到与1重合的点对应的坐标是（　　）
    A、
    k
    2n
    (k    为[1，2n]中所有奇数）
    B、
    2k+1
    2n
    (k∈N*，且k≤n)
    C、
    k
    2n-1
    (k    为[1，2n-1]中所有奇数）
    D、
    2k-1
    2n
    (k∈N*，且k≤n)

    查看答案和解析>>

    定义：平面内两条相交但不垂直的数轴构成的坐标系（两条数轴的原点重合且单位长度相同）称为平面斜坐标系；在平面斜坐标系中，若（其中、分别是斜坐标系轴、轴正方向上的单位向量，，为坐标原点），则有序实数对称为点的斜坐标. 如图所示,在平面斜坐标系中，若，点，为单位圆上一点，且，点在平面斜坐标系中的坐标是

    A. 

    B. 

     C. 

     D.

     

    查看答案和解析>>


    同步练习册答案