
题目列表(包括答案和解析)
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
|
|
| a | 2 1 |
| a | 2 2 |
| a | 2 3 |
| b | 2 1 |
| b | 2 2 |
| b | 2 3 |
| x |
| 2x-2 |
| 8-3x |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
|
|
| a | 21 |
| a | 22 |
| a | 23 |
| b | 21 |
| b | 22 |
| b | 23 |
| x |
| 2x-2 |
| 8-3x |
已知函数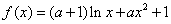 .
.
(Ⅰ)讨论函数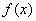 的单调性;
的单调性;
(Ⅱ)设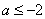 ,证明:对任意
,证明:对任意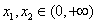 ,
,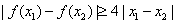 .
.
 1.选修4-1:几何证明选讲
1.选修4-1:几何证明选讲
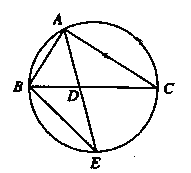
如图, 的角平分线
的角平分线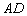 的延长线交它的外接圆于点
的延长线交它的外接圆于点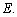
(Ⅰ)证明: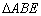 ∽△
∽△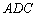 ;
;
(Ⅱ)若 的面积
的面积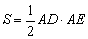 ,求
,求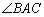 的大小.
的大小.
证明:(Ⅰ)由已知条件,可得∠BAE=∠CAD.
因为∠AEB与∠ACB是同弧上的圆周角,所以∠AEB=∠ACD.
故△ABE∽△ADC.
(Ⅱ)因为△ABE∽△ADC,所以 ,即AB·AC=AD·AE.
,即AB·AC=AD·AE.
又S= AB·ACsin∠BAC,且S=
AB·ACsin∠BAC,且S= AD·AE,故AB·ACsin∠BAC=AD·AE.
AD·AE,故AB·ACsin∠BAC=AD·AE.
则sin∠BAC=1,又∠BAC为三角形内角,所以∠BAC=90°.
请先阅读:
设平面向量![]() =(a1,a2),
=(a1,a2),![]() =(b1,b2),且
=(b1,b2),且![]() 与
与![]() 的夹角为è,
的夹角为è,
因为![]() •
•![]() =|
=|![]() ||
||![]() |cosè,
|cosè,
所以![]() •
•![]() ≤|
≤|![]() ||
||![]() |.
|.
即![]() ,
,
当且仅当è=0时,等号成立.
(I)利用上述想法(或其他方法),结合空间向量,证明:对于任意a1,a2,a3,b1,b2,b3∈R,都有![]() 成立;
成立;
(II)试求函数![]() 的最大值.
的最大值.
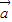 =(a1,a2),
=(a1,a2),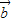 =(b1,b2),且
=(b1,b2),且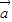 与
与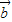 的夹角为θ,
的夹角为θ,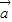 •
•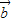 =|
=|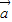 ||
||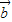 |cosθ,
|cosθ,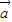 •
•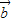 ≤|
≤|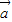 ||
||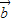 |.
|.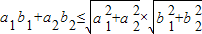 ,
,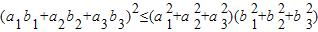 成立;
成立;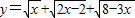 的最大值.
的最大值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com