如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1.

（Ⅰ）证明PC⊥AD；

（Ⅱ）求二面角A-PC-D的正弦值；

（Ⅲ）设E为棱PA上的点，满足异面直线BE与CD所成的角为30°，求AE的长.

【解析】解法一：如图，以点A为原点建立空间直角坐标系，依题意得A(0,0,0)，D(2,0,0),C(0,1,0), 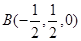,P（0,0,2）.

（1）证明：易得，于是,所以

(2) ,设平面PCD的法向量，

则,即.不防设，可得.可取平面PAC的法向量于是从而.

所以二面角A-PC-D的正弦值为.

（3）设点E的坐标为（0,0，h），其中，由此得.

由，故 

所以，，解得，即.

解法二：（1）证明：由，可得，又由,,故.又,所以.

(2)如图，作于点H，连接DH.由,,可得.

因此,从而为二面角A-PC-D的平面角.在中，,由此得由（1）知,故在中，

因此所以二面角的正弦值为.

（3）如图，因为，故过点B作CD的平行线必与线段AD相交，设交点为F，连接BE，EF. 故或其补角为异面直线BE与CD所成的角.由于BF∥CD，故.在中，故

在中，由,,

可得.由余弦定理，,

所以.

如图6，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是等腰梯形，AD∥BC，AC⊥BD.

（Ⅰ）证明：BD⊥PC；

（Ⅱ）若AD=4，BC=2，直线PD与平面PAC所成的角为30°，求四棱锥P-ABCD的体积.

【解析】（Ⅰ）因为

又是平面PAC内的两条相较直线，所以BD平面PAC，

而平面PAC，所以.

（Ⅱ）设AC和BD相交于点O，连接PO，由（Ⅰ）知，BD平面PAC，

所以是直线PD和平面PAC所成的角，从而.

由BD平面PAC，平面PAC，知.在中，由，得PD=2OD.因为四边形ABCD为等腰梯形，，所以均为等腰直角三角形，从而梯形ABCD的高为于是梯形ABCD面积

在等腰三角形ＡＯＤ中，

所以

故四棱锥的体积为.

【点评】本题考查空间直线垂直关系的证明，考查空间角的应用，及几何体体积计算.第一问只要证明BD平面PAC即可，第二问由（Ⅰ）知，BD平面PAC，所以是直线PD和平面PAC所成的角，然后算出梯形的面积和棱锥的高，由算得体积

已知函数其中为自然对数的底数， .(Ⅰ)设，求函数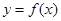的最值；（Ⅱ）若对于任意的，都有成立，求的取值范围.

【解析】第一问中，当时，，．结合表格和导数的知识判定单调性和极值，进而得到最值。

第二问中，∵，，      

∴原不等式等价于：,

即, 亦即

分离参数的思想求解参数的范围

解：（Ⅰ)当时，，．

当在上变化时，，的变化情况如下表：

∴时，，．

(Ⅱ)∵，，      

∴原不等式等价于：,

即, 亦即．

∴对于任意的，原不等式恒成立,等价于对恒成立,

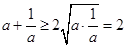∵对于任意的时, （当且仅当时取等号）．

∴只需，即，解之得或.

因此，的取值范围是

已知函数，

（1）求函数的定义域；

（2）求函数在区间上的最小值；

（3）已知，命题p：关于x的不等式对函数的定义域上的任意恒成立；命题q：指数函数是增函数．若“p或q”为真，“p且q”为假，求实数m的取值范围．

【解析】第一问中，利用由 即

第二问中，，得：

，

第三问中，由在函数的定义域上 的任意，，当且仅当时等号成立。当命题p为真时，；而命题q为真时：指数函数．因为“p或q”为真，“p且q”为假，所以

当命题p为真，命题q为假时；当命题p为假，命题q为真时分为两种情况讨论即可 。

解：（1）由 即

（2），得：

，

（3）由在函数的定义域上 的任意，，当且仅当时等号成立。当命题p为真时，；而命题q为真时：指数函数．因为“p或q”为真，“p且q”为假，所以

当命题p为真，命题q为假时，

当命题p为假，命题q为真时，，

所以