
题目列表(包括答案和解析)
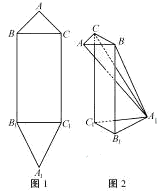 平面图形ABB2A2C3C如图4所示,其中BB1C1C是矩形,BC=2,BB1=4,AB=AC=
平面图形ABB2A2C3C如图4所示,其中BB1C1C是矩形,BC=2,BB1=4,AB=AC= ,A1B1=A1C1=
,A1B1=A1C1= .现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
.现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题. 如图4所示,其中
如图4所示,其中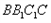 是矩形,
是矩形,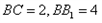 ,
,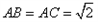 ,
, 。现将该平面图形分别沿
。现将该平面图形分别沿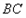 和
和 折叠,使
折叠,使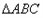 与
与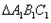 所在平面都与平面
所在平面都与平面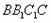 垂直,再分别连接
垂直,再分别连接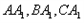 ,得到如图2所示的空间图形,对此空间图形解答下列问题。
,得到如图2所示的空间图形,对此空间图形解答下列问题。
 ;
;  的长;
的长; 的余弦值。
的余弦值。平面图形![]() 如图4所示,其中
如图4所示,其中![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() 。现将该平面图形分别沿
。现将该平面图形分别沿![]() 和
和![]() 折叠,使
折叠,使![]() 与
与![]() 所在平面都与平面
所在平面都与平面![]() 垂直,再分别连接
垂直,再分别连接![]() ,得到如图2所示的空间图形,对此空间图形解答下列问题。
,得到如图2所示的空间图形,对此空间图形解答下列问题。
 。
。
(Ⅰ)证明:![]() ; (Ⅱ)求
; (Ⅱ)求![]() 的长;
的长;
(Ⅲ)求二面角![]() 的余弦值。
的余弦值。
平面图形![]() 如图4所示,其中
如图4所示,其中![]() 是矩形,
是矩形,![]() ,
,![]() ,
,
![]() 。现将该平面图形分别沿
。现将该平面图形分别沿![]() 和
和![]() 折叠,使
折叠,使![]() 与
与![]() 所在平面都
所在平面都
与平面![]() 垂直,再分别连接
垂直,再分别连接![]() ,得到如图2所示的空间图形,对此空间图形解答
,得到如图2所示的空间图形,对此空间图形解答
下列问题。
 。
。
(Ⅰ)证明:![]() ; (Ⅱ)求
; (Ⅱ)求![]() 的长;
的长;
(Ⅲ)求二面角![]() 的余弦值。
的余弦值。
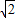 ,A1B1=A1C1=
,A1B1=A1C1=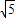 .现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
.现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.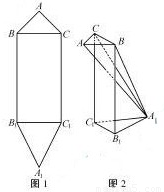
说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.
2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,选择题和填空题不给中间分.
一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.
题号
1
2
3
4
5
6
7
8
答案
A
B
C
D
A
C
B
D
二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,每小题5分,满分30分.其中13~15是选做题,考生只能选做两题. 第12题第一个空2分,第二个空3分.
9. 10.
10. 11.
11. 12.-1;4 13.
12.-1;4 13.
14.1 15. 
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
(本小题主要考查正弦定理、余弦定理、同角三角函数的基本关系等基础知识,考查运算求解能力)
解: (1)∵ , 且
, 且 ,
,
∴  .
.
由正弦定理得 .
.
∴ .
.
(2)∵
∴ .
.
∴  .
.
由余弦定理得 ,
,
∴ .
.
17.(本小题满分14分)
(本小题主要考查概率、随机变量的分布列及其数学期望等基础知识,考查运算求解能力)
解:(1)记“甲射击一次,击中目标”为事件 ,“乙射击一次,击中目标”为事件
,“乙射击一次,击中目标”为事件 ,“甲射击一次,
,“甲射击一次,
未击中目标”为事件 ,“乙射击一次,未击中目标”为事件
,“乙射击一次,未击中目标”为事件 ,
,
则 ,
, .
.
依题意得 ,
,
解得 .
.
故 的值为
的值为 .
.
(2) 的取值分别为
的取值分别为 .
.
 ,
,
 ,
,
 ,
,
 的分布列为
的分布列为

0
2
4







18.(本小题满分14分)
 (本小题主要考查空间中线面的位置关系、空间的角、几何体体积等基础知识,考查空间想象能力、推理论证能力和运算求解能力)
(本小题主要考查空间中线面的位置关系、空间的角、几何体体积等基础知识,考查空间想象能力、推理论证能力和运算求解能力)
(1)
证明: ∵ 分别是棱
分别是棱 的中点,
的中点,
∴ 是△
是△ 的中位线.
的中位线.
∴ .
.
∵ 平面
平面 平面
平面
∴ 平面
平面 .
.
同理可证  平面
平面 .
.
∵ 平面
平面 ,
, 平面
平面 ,
,
∴平面 // 平面
// 平面 .
.
(2) 求三棱锥 的体积的最大值, 给出如下两种解法:
的体积的最大值, 给出如下两种解法:
解法1: 由已知 平面
平面 ,
,  ,
,
∴ .
.
∴三棱锥 的体积为
的体积为




 .
.
当且仅当 时等号成立,
时等号成立, 取得最大值,其值为
取得最大值,其值为 , 此时
, 此时
 .
.
解法2:设 ,在Rt△
,在Rt△ 中,
中,
 .
.
∴三棱锥 的体积为
的体积为



 .
.
∵ ,
,
∴ 当 ,即
,即 时,
时, 取得最大值,其值为
取得最大值,其值为 ,此时
,此时 .
.
求二面角 的平面角的余弦值, 给出如下两种解法:
的平面角的余弦值, 给出如下两种解法:
解法1:作 ,垂足为
,垂足为 , 连接
, 连接 .
.
∵  平面
平面 ,平面
,平面 平面
平面 ,
,
∴  平面
平面 .
.
∵  平面
平面 ,
,
∴ 
 .
.
∵  ,
,
∴  平面
平面 .
.
∵ 平面
平面 ,
,
∴
 .
.
∴  是二面角
是二面角 的平面角.
的平面角.
 在Rt△
在Rt△ 中,
中, ,
,
∴ .
.
在Rt△ 中,
中, ,
,
 .
.
∴二面角 的平面角的余弦值为
的平面角的余弦值为 .
.
解法2:分别以 所在直线为
所在直线为 轴,
轴,  轴,
轴,  轴,建立如图的空间直角坐标系
轴,建立如图的空间直角坐标系 ,
,
 则
则 .
.
∴ .
.
设n 为平面
为平面 的法向量,
的法向量,
∴
即
令 , 则
, 则 .
.
∴
 为平面
为平面 的一个法向量.
的一个法向量.
∵平面 的一个法向量为
的一个法向量为 ,
,
∴ .
.
∴二面角 的平面角的余弦值为
的平面角的余弦值为 .
.
19.(本小题满分12分)
(本小题主要考查函数最值、不等式、导数及其应用等基础知识,考查分类与整合的数学思想方法,以及运算求解能力和应用意识)
解:(1)生产150件产品,需加工 型零件450个,
型零件450个,
则完成 型零件加工所需时间
型零件加工所需时间
 N
N ,且
,且 .
.
(2)生产150件产品,需加工 型零件150个,
型零件150个,
则完成 型零件加工所需时间
型零件加工所需时间
 N
N ,且
,且 .
.
设完成全部生产任务所需时间为 小时,则
小时,则 为
为 与
与 的较大者.
的较大者.
令 ,即
,即 ,
,
解得 .
.
所以,当 时,
时, ;当
;当 时,
时, .
.
故 .
.
当 时,
时, ,故
,故 在
在 上单调递减,
上单调递减,
则 在
在 上的最小值为
上的最小值为 (小时);
(小时);
当 时,
时, ,故
,故 在
在 上单调递增,
上单调递增,
则 在
在 上的最小值为
上的最小值为 (小时);
(小时);
 ,
,

 在
在 上的最小值为
上的最小值为 .
.
 .
.
答:为了在最短时间内完成生产任务, 应取
应取 .
.
20.(本小题满分14分)
(本小题主要考查圆、椭圆、直线等基础知识和数学探究,考查数形结合、分类与整合的数学思想方法,以及推理论证能力、运算求解能力和创新意识)
解:(1)圆 , 圆心
, 圆心 的坐标为
的坐标为 ,半径
,半径 .
.
∵ ,
,
∴点 在圆
在圆 内.
内.
设动圆 的半径为
的半径为 ,圆心为
,圆心为 ,依题意得
,依题意得 ,且
,且 ,
,
即 .
.
∴圆心 的轨迹是中心在原点,以
的轨迹是中心在原点,以 两点为焦点,长轴长为
两点为焦点,长轴长为 的椭圆,设其方程为
的椭圆,设其方程为
 , 则
, 则 .
.
∴ .
.
∴所求动圆 的圆心的轨迹方程为
的圆心的轨迹方程为 .
.
(2)由 消去
消去 化简整理得:
化简整理得: .
.
设 ,
, ,则
,则 .
.
△
 . ①
. ①
由 消去
消去 化简整理得:
化简整理得: .
.
设 ,则
,则 ,
,
△
 . ②
. ②
∵ ,
,
∴ ,即
,即 ,
,
∴ .
.
∴ 或
或 .
.
解得 或
或 .
.
当 时,由①、②得
时,由①、②得  ,
,
∵ Z,
Z,
∴ 的值为
的值为
 ,
, ,
,
 ;
;
当 ,由①、②得
,由①、②得  ,
,
∵ Z,
Z,
∴ .
.
∴满足条件的直线共有9条.
21.(本小题满分14分)
(本小题主要考查数列的通项公式、数列前 项和、不等式等基础知识,考查化归与转化、分类与整合、特殊与一般的数学思想方法,以及推理论证能力、运算求解能力和抽象概括能力)
项和、不等式等基础知识,考查化归与转化、分类与整合、特殊与一般的数学思想方法,以及推理论证能力、运算求解能力和抽象概括能力)
解: (1) ∵ 是关于
是关于 的方程
的方程
 N
N 的两根,
的两根,
∴
求数列 的通项公式, 给出如下四种解法:
的通项公式, 给出如下四种解法:
解法1: 由 ,得
,得 ,
,
故数列 是首项为
是首项为 ,公比为
,公比为 的等比数列.
的等比数列.
∴ , 即
, 即 .
.
解法2: 由 ,两边同除以
,两边同除以 , 得
, 得 ,
,
令 , 则
, 则 .
.
故



 .
.
且 也适合上式,
也适合上式,
∴
 , 即
, 即 .
.
解法3: 由 ,得
,得 ,
,
两式相减得 .
.
当 为正奇数时,
为正奇数时,



 .
.
且 也适合上式.
也适合上式.
当 为正偶数时,
为正偶数时,



 .
.
且 也适合上式.
也适合上式.
∴
当 N
N 时,
时,
 .
.
解法4:由 ,
, ,得
,得
 ,
,
 .
.
猜想
 .
.
下面用数学归纳法证明猜想正确.
① 当 时,易知猜想成立;
时,易知猜想成立;
② 假设当
 N
N )时,猜想成立,即
)时,猜想成立,即 ,
,
由 ,得
,得 ,
,
故当 时,猜想也成立.
时,猜想也成立.
由①、②得,对任意 N
N ,
,
 .
.
∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com