
题目列表(包括答案和解析)
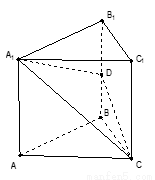
如图,在直三棱柱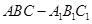 中,底面
中,底面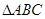 为等腰直角三角形,
为等腰直角三角形,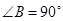 ,
,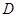 为棱
为棱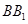 上一点,且平面
上一点,且平面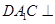 平面
平面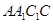 .
.
(Ⅰ)求证: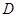 点为棱
点为棱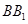 的中点;
的中点;
(Ⅱ)判断四棱锥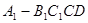 和
和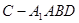 的体积是否相等,并证明。
的体积是否相等,并证明。
【解析】本试题主要考查了立体几何中的体积问题的运用。第一问中,
易知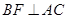 ,
,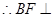 面
面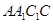 。由此知:
。由此知: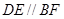 从而有
从而有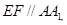 又点
又点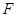 是
是 的中点,所以
的中点,所以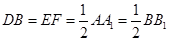 ,所以
,所以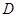 点为棱
点为棱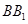 的中点.
的中点.
(2)中由A1B1⊥平面B1C1CD,BC⊥平面A1ABD,D为BB1中点,可以得证。
(1)过点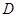 作
作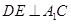 于
于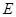 点,取
点,取 的中点
的中点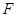 ,连
,连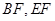 。
。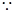 面
面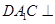 面
面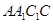 且相交于
且相交于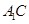 ,面
,面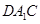 内的直线
内的直线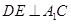 ,
,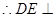 面
面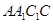 。……3分
。……3分
又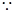 面
面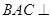 面
面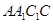 且相交于
且相交于 ,且
,且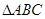 为等腰三角形,易知
为等腰三角形,易知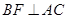 ,
,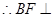 面
面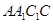 。由此知:
。由此知: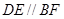 ,从而有
,从而有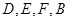 共面,又易知
共面,又易知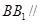 面
面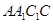 ,故有
,故有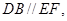 从而有
从而有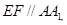 又点
又点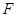 是
是 的中点,所以
的中点,所以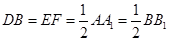 ,所以
,所以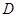 点为棱
点为棱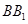 的中点.
…6分
的中点.
…6分
(2)相等.ABC-A1B1C1为直三棱柱,∴BB1⊥A1B1,BB1⊥BC,又A1B1⊥B1C1,BC⊥AB,
∴A1B1⊥平面B1C1CD,BC⊥平面A1ABD(9分)∴VA1-B1C1CD=1 /3 SB1C1CD•A1B1=1/ 3 ×1 2 (B1D+CC1)×B1C1×A1B1VC-A1ABD=1 /3 SA1ABD•BC=1 /3 ×1 2 (BD+AA1)×AB×BC∵D为BB1中点,∴VA1-B1C1CD=VC-A1ABD
如图,三棱柱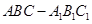 中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。
中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。
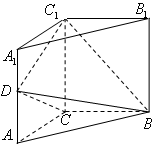
(I) 证明:平面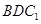 ⊥平面
⊥平面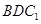
(Ⅱ)平面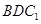 分此棱柱为两部分,求这两部分体积的比.
分此棱柱为两部分,求这两部分体积的比.
【命题意图】本题主要考查空间线线、线面、面面垂直的判定与性质及几何体的体积计算,考查空间想象能力、逻辑推理能力,是简单题.
【解析】(Ⅰ)由题设知BC⊥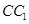 ,BC⊥AC,
,BC⊥AC,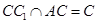 ,∴
,∴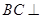 面
面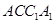 , 又∵
, 又∵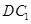
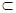 面
面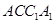 ,∴
,∴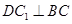 ,
,
由题设知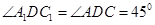 ,∴
,∴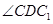 =
=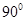 ,即
,即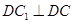 ,
,
又∵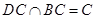 , ∴
, ∴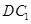 ⊥面
⊥面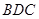 , ∵
, ∵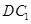
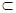 面
面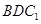 ,
,
∴面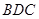 ⊥面
⊥面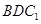 ;
;
(Ⅱ)设棱锥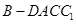 的体积为
的体积为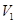 ,
,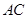 =1,由题意得,
=1,由题意得,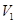 =
=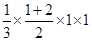 =
=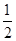 ,
,
由三棱柱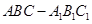 的体积
的体积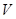 =1,
=1,
∴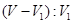 =1:1, ∴平面
=1:1, ∴平面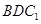 分此棱柱为两部分体积之比为1:1
分此棱柱为两部分体积之比为1:1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com