
题目列表(包括答案和解析)
(本小题满分13分)有一问题,在半小时内,甲能解决它的概率是0.5,乙能解决它的概率是![]() ,
,
如果两人都试图独立地在半小时内解决它,计算:w.w.w.k.s.5.u.c.o.m ![]()
![]()
(1)两人都未解决的概率;
(2)问题得到解决的概率。
(本小题满分13分) 已知![]() 是等比数列,
是等比数列,![]() ;
;![]() 是等差数列,
是等差数列,![]() ,
,![]() .
.
(1) 求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2) 设![]() +…+
+…+![]() ,
,![]() …
…![]() ,其中
,其中![]() ,…试比较
,…试比较![]() 与
与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
(本小题满分13分) 现有一批货物由海上从A地运往B地,已知货船的最大航行速度为35海里/小时,A地至B地之间的航行距离约为500海里,每小时的运输成本由燃料费和其余费用组成,轮船每小时的燃料费用与轮船速度的平方成正比(比例系数为0.6),其余费用为每小时960元.
(1)把全程运输成本y(元)表示为速度x(海里/小时)的函数;
(2)为了使全程运输成本最小,轮船应以多大速度行驶?
(本小题满分13分)
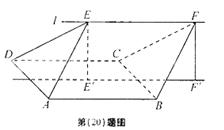
如图,ABCD的边长为2的正方形,直线l与平面ABCD平行,g和F式l上的两个不同点,且EA=ED,FB=FC, ![]() 和
和![]() 是平面ABCD内的两点,
是平面ABCD内的两点,![]() 和
和![]()
![]() 都与平面ABCD垂直,
都与平面ABCD垂直,
(Ⅰ)证明:直线![]() 垂直且平分线段AD:w.w.w.k.s.5.u.c.o.m
垂直且平分线段AD:w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅱ)若∠EAD=∠EAB=60°,EF=2,求多面
体ABCDEF的体积。
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个答案中,只有一个项是符合题目要求的,把正确的代号填在答题卡指定的位置上。
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
C
A
A
A
D
B
D
C
二、填空题:本大题共5小题,每小题4分,共20分,把答案填在答题卡的相应位置。
11.-1或 12.
12.
14.  15.100100
15.100100
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤,在答题卡上相应题目的答题区域内作答。
16. (本小题满分13分)
解:

两边平方并整理得


根据余弦定理得
17. (本小题满分13分)
解法一:
(Ⅰ)由俯视图可得:

有俯视图知

故 是以B为直角顶点的直角三角形。
是以B为直角顶点的直角三角形。
(Ⅱ)三角形PAC的面积为
 俯视图是底边长为
俯视图是底边长为 ,斜边上的高为
,斜边上的高为 的等腰直角三角形
的等腰直角三角形
 三角形PAB的面积为
三角形PAB的面积为 ,且PB=
,且PB=
由(Ⅰ)知三角形PBC是直角三角形,故其面积为
故三棱锥P-ABC的全面积为
(Ⅲ)在面ABC内过A做AC的垂线AQ,
以A为原点,AC、AQ、AP所在直线分别为x轴、y轴 、z轴建立空间直角坐标系,如图所示
则
 设
设 为面PAB的一个法向量
为面PAB的一个法向量
则
 取
取 设
设


故当E为PC的中点时,AE与面PAB所成的为600
解法二:
(Ⅰ)由正视图和俯视图可判断

在面ABC内过A做AC的垂线AQ
以A为原点,AC、AQ、AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示
则


故 是以B为直角顶点的直角三角形。
是以B为直角顶点的直角三角形。
(Ⅱ)同解法一。
(Ⅲ)设 为面PAB的一个法向量
为面PAB的一个法向量
则 取
取


故当E为PC的中点时,AE与面PAB所成的为600
18. (本小题满分13分)
解:
(Ⅰ)设抽到相邻两个月的数据为事件A
因为从6组数据中选取2组数据共有 中情况,每种情况都是等可能出现的其中,抽到相邻两个月的数据的情况有5种
中情况,每种情况都是等可能出现的其中,抽到相邻两个月的数据的情况有5种
所以
(Ⅱ)由数据求得
由公式求得
再由
所以y关于x的线性回归方程为
(Ⅲ)当 时,
时,
同样,当 时,
时,
所以,该小组所得线性回归方程是理想的。
19. (本小题满分13分)‘
解:(Ⅰ)设椭圆方程为
 ①
①
 点A(1,1)在椭圆上,
点A(1,1)在椭圆上, ②
②
又 ③
③
故所求椭圆方程为
(Ⅱ)由A(1,1)得C(-1,1)
则
易知AP的斜率k必存在,设AP; 则
则
由
由A(1,1)得 的一个根
的一个根
由韦达定理得:
以-k代k得


故
即存在实数
20. (本小题满分14分)
解:(Ⅰ)

当 时,
时,
当 时,
时,
故 连续,故
连续,故
(Ⅱ) 即不等式
即不等式 在区间
在区间 有解
有解
 可化为
可化为
 在区间
在区间 有解
有解
令
 故
故 在区间
在区间 递减,在区间
递减,在区间 递增
递增
又
所以,实数a的取值范围为
(Ⅲ)设存在公差为d首项等于 的等差数列
的等差数列
和公比q大于0的等比数列 ,使得数列
,使得数列 的前n项和等于
的前n项和等于

故
即 ①
①
 ②
②
②-①×2得
 (舍去)
(舍去)
故 ,
,
此时, 数列
数列 的的前n项和等于
的的前n项和等于

故存在满足题意的等差数列 金额等比数列
金额等比数列 ,使得数列
,使得数列 的前n项和等于
的前n项和等于
21. 本题有(1)、(2)、(3)三个小题,每题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分
(1)(本小题满分7分)选修4――2:矩阵与变换
解一:
设

解二:
设  则
则
故
(2)(本小题满分7分)选修4――4:坐标系与凡属方程
解:曲线C1可化为:
曲线C2可化为
联立 解得交点为
解得交点为
(3)(本小题满分7分)选修4――5:不等式选讲
解:
当且仅当
 取最小值,最小值为
取最小值,最小值为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com