查看答案和解析>>

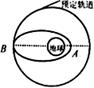
(8分)我国“神舟”号飞船由运载火箭送入近地点为A、远地点为B的椭圆轨道上．近地点A距地面高度为h₁，实施变轨后，进入预定圆轨道，如图所示．在预定圆轨道上飞行n圈所用时间为t，之后返回．已知地球表面重力加速度为g，地球半径为R，求：
(1)飞船在近地点A的加速度为多大?
(2)远地点B距地面的高度为多少?

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

题号

1

2

3

4

5

6

7

8

9

10

11

12

答案

B

C

CD

A

B

B

C

AD

BD

D

C

D

13.（1）2.030（2分）       （2）75.2s（1分）1.88s  （1分）

（3）例如：计算摆长时，漏加摆球半径等于合理答案均给分。（2分）

14.  （由于实验操作顺序原因而写成）

15.解：（1）根据动能定理可求带电粒子刚进入偏转管C时的瞬时速度

由 得     ①

（2）电场力提供了带电粒子在偏转管C内运动所需的向心力

       ②

由①②式得       （2分）

16.解：（1）设地球质量为.飞船质量为,则地球表面质量为的某物体

, 所以    ①

飞船在A点受到地球引力为   ②

由①②得

（2）飞船在预定圆轨道飞行的周期

根据牛顿第二定律

解得

17.解：根据牛顿第二定律可知滑块A在斜面上下滑的加速度

   ①

设A到斜面底部的速度为，所经时间为

     ②

当A恰好追上滑块B时，滑块A在水平底部经时间

     ③

当A恰好能追上滑块B， 滑块B的速度恰好等于，即

    ④

由①②③④解方程组得

18.解因为，所以粒子通过磁场的时间小于周期

由于得     ①      由于得      ②

（1）当弦长最短，即由P进入Q飞出时，离子在磁场中运动时间最短

            ③

从几何关系可知       ④

由①②③④得     

（2）当速度沿界面I竖直向上时，离子在磁场中运动时间最长，

从几何关系可知

           ⑤            ⑥

  ⑦            由于    ⑧

由①②③④⑤⑥⑦⑧得

解法二：由得

同理可得

19.解：（1）根据法拉第电磁感应定律可求三段的感应电动势

根据闭合电路欧姆定律求出bc两点间的电势差

金属板间的电势差为

由平衡条件可得

（2）金属棒所受安培力为

加在金属棒上拉力的功率

 20.解：（1）根据机械能守恒定律  

得物体P滑到B点时的速度为 

（2）没有传送带时，物块离开B点后做平抛运动的时间为t:物块从静止的传送带右端水平抛出，在空中运动的时间也为：  

水平位移为，因此物体从传送带右端抛出的速度

根据动能定理

所以传送带之间的动摩擦因数为

（3）当传送带向右运动时，若传送带的速度，即时，物体在传送带上一直做匀减速运动，离开传送带的速度仍为，落地的水平位移为，即

当传送带的速度时，物体将会在传送带上先做一段匀变速运动，如果尚未到达传送带右端，速度即与传送带速度相同，此后物体将做匀速运动，而后以速度离开传送带，的最大值为物体在传送带上一直加速而达到的速度。

  由此解得

当，物体将以速度离开传送带，因此得O、D之间的距离为

当，即时，物体从传送带右端飞出时的速度为，O、D之间的距离为   

综合以上的结果，得出O、D之间的距离s随速度变化的函数关系为