
题目列表(包括答案和解析)
(本题14分)向量 ,设函数
,设函数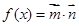 .
.
(1)求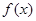 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在 中,
中,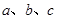 分别是角
分别是角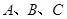 的对边,若
的对边,若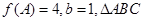 的面积
的面积
为 ,求a的值.
,求a的值.
(本题14分)
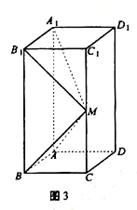
如图所示,在长方体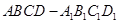 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点
(1)求异面直线A1M和C1D1所成的角的正切值;
(2)证明:直线BM⊥平面A1B1M1
(本题14分)已知a,b实数,设函数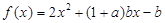 .
.
(1)若关于x的不等式 的解集为
的解集为 ,求实数
,求实数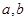 的值;
的值;
(2) 设b为已知的常数,且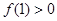 ,求满足条件的a的范围.
,求满足条件的a的范围.
(本题14分)如图,一水渠的横断面是抛物线形,O是抛物线的顶点,口宽EF=4米,高3米,建立适当的直角坐标系,(1)求抛物线方程.(2)若将水渠横断面改造成等腰梯形ABCD,要求高度不变,只挖土,不填土,求梯形ABCD的下底AB多大时,所挖的土最少? 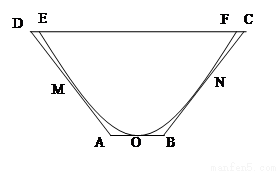
(本题14分)口袋内有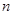 (
(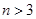 )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和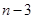 个白球.已知从
个白球.已知从
口袋中随机取出一个球是红球的概率是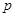 ,且
,且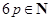 。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于
。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于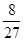 。
。
(Ⅰ)求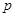 和
和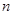 ;
;
(Ⅱ)不放回地从口袋中取球(每次只取一个球),取到白球时即停止取球,记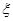 为第一次取到白球时的取球次数,求
为第一次取到白球时的取球次数,求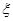 的分布列和期望
的分布列和期望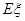 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com