
题目列表(包括答案和解析)
(本题12分)
某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按 A类、B类分二层)从该年级的学生中共抽查100名同学,如果以身高达165cm作为达标的标准,对抽取的100名学生,得到以下列联表:
体育锻炼与身高达标2×2列联表
|
|
身高达标 |
身高不达标 |
总计 |
|
积极参加 体育锻炼 |
40 |
|
|
|
不积极参加 体育锻炼 |
|
15 |
|
|
总计 |
|
|
100 |
(1)完成上表;
(2)请问有多大的把握认为体育锻炼与身高达标有关系(K2值精确到0.01)?
参考公式:K2=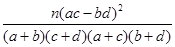 ,参考数据:
,参考数据:
|
P(K2≥k0) |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
|
K0 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
(本题满分12分)某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
数学 成绩 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
83 |
72 |
83 |
|
物理 成绩 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
81 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
84 |
78 |
86 |
若单科成绩85分以上(含85分),则该科成绩为优秀.
(1)根据上表完成下面的2×2列联表(单位:人):
|
|
数学成绩优秀 |
数学成绩不优秀 |
合 计 |
|
物理成绩优秀 |
|
|
|
|
物理成绩不优秀 |
|
|
|
|
合 计 |
|
|
20 |
(2)根据题(1)中表格的数据计算,有多大的把握,认为学生的数学成绩与物理成绩之间有关系?
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考数据及公式:
①随机变量 ,其中
,其中 为样本容量;
为样本容量;
②独立检验随机变量 的临界值参考表:
的临界值参考表:
|
|
0.010 |
0.005 |
0.001 |
|
|
6.635 |
7.879 |
10.828 |
(本题满分14分)
某校高三的某次数学测试中,对其中100名学生的成绩进行分析,按成绩分组,得到的频率分布表如下:
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
|
15 |
① |
|
第2组 |
|
② |
0.35 |
|
第3组 |
|
20 |
0.20 |
|
第4组 |
|
20 |
0.20 |
|
第5组 |
|
10 |
0.10 |
|
合计 |
|
100 |
1.00 |
(1)求出频率分布表中①、②位置相应的数据;
(2)为了选拔出最优秀的学生参加即将举行的数学竞赛,学校决定在成绩较高的第3、4、5组中分层抽样取5名学生,则第4、5组每组各抽取多少名学生?
(3)为了了解学生的学习情况,学校又在这5名学生当中随机抽取2名进行访谈,求第4组中至少有一名学生被抽到的概率是多少?
(本题满分15分)
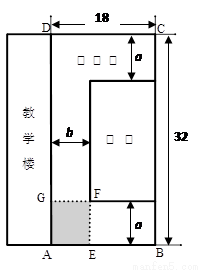
如图所示,某学校的教学楼前有一块矩形空地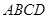 ,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为
,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为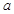 米与
米与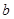 米均不小于2米,且要求“转角处”(图中矩形
米均不小于2米,且要求“转角处”(图中矩形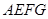 )的面积为8平方米
)的面积为8平方米
(1) 试用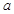 表示草坪的面积
表示草坪的面积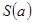 ,并指出
,并指出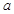 的取值范围
的取值范围
(2) 如何设计人行道的宽度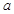 、
、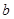 ,才能使草坪的面积最大?并求出草坪的最大面积。
,才能使草坪的面积最大?并求出草坪的最大面积。
(本题满分12分)
某学校的课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
若单科成绩在85分以上(含85分),则该科成绩为优秀.
(1)根据上表完成下面的![]() 列联表(单位:人)
列联表(单位:人)
| 数学成绩优秀 | 数学成绩不优秀 | 总计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | |||
| 总计 | 20 |
(2)根据(1)中表格的数据计算,是否有99%的把握,认为学生的数学成绩与物理成绩之间有关系?
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考公式:![]()
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com