
题目列表(包括答案和解析)
(本小题满分12分)
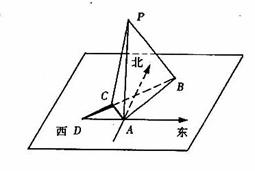
在海岛A上有一座海拔![]() 千米的山,山顶设有一个观察站P,上午11时,测得一轮船在海岛北偏东30°,俯角为30°的B处。到11时10分又测得该船在岛北偏西60°,俯角为60°的C处。
千米的山,山顶设有一个观察站P,上午11时,测得一轮船在海岛北偏东30°,俯角为30°的B处。到11时10分又测得该船在岛北偏西60°,俯角为60°的C处。
(Ⅰ)该船的航行速度是每小时多千米?
(Ⅱ)又经过一段时间后,船到达海岛正西方向的D处,此时船距岛有多远?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com