
题目列表(包括答案和解析)
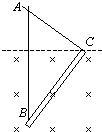 如图所示,AB为竖直固定金属棒,金属杆BC重为G.长为L,并可绕过B点垂直纸面的水平轴无摩擦转动,AC为轻质金属线,∠ABC=37°,∠ACB=90°,在图示范围内有一匀强磁场,其磁感应强度与时间成正比:B=k t,整个回路总电阻为R,则回路中感应电流I=
如图所示,AB为竖直固定金属棒,金属杆BC重为G.长为L,并可绕过B点垂直纸面的水平轴无摩擦转动,AC为轻质金属线,∠ABC=37°,∠ACB=90°,在图示范围内有一匀强磁场,其磁感应强度与时间成正比:B=k t,整个回路总电阻为R,则回路中感应电流I=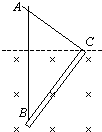
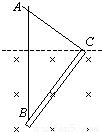
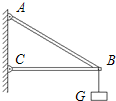 如图所示,在用轻杆制作的三角形支架的B点悬挂一个重为150N的重物G.已知:AB:BC:AC=5:4:3,则横梁BC和斜梁AB所受的力的大小分别为( )
如图所示,在用轻杆制作的三角形支架的B点悬挂一个重为150N的重物G.已知:AB:BC:AC=5:4:3,则横梁BC和斜梁AB所受的力的大小分别为( ) 如图所示,A点是一个固定的铰链,AB是一根轻杆,与竖直墙壁AC成30°角,BC是一根不可伸长的轻绳,方向水平,所挂物体的质量为m,试求AB杆中的弹力和BC绳中的张力大小.
如图所示,A点是一个固定的铰链,AB是一根轻杆,与竖直墙壁AC成30°角,BC是一根不可伸长的轻绳,方向水平,所挂物体的质量为m,试求AB杆中的弹力和BC绳中的张力大小.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com