
题目列表(包括答案和解析)
已知函数 ,(
,(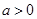 ),
),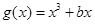
(1)若曲线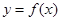 与曲线
与曲线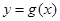 在它们的交点(1,c)处具有公共切线,求a,b的值
在它们的交点(1,c)处具有公共切线,求a,b的值
(2)当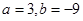 时,若函数
时,若函数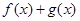 在区间[k,2]上的最大值为28,求k的取值范围
在区间[k,2]上的最大值为28,求k的取值范围
【解析】(1)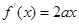 ,
,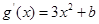
∵曲线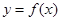 与曲线
与曲线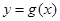 在它们的交点(1,c)处具有公共切线
在它们的交点(1,c)处具有公共切线
∴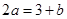 ,
,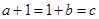
∴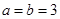
(2)当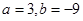 时,
时,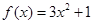 ,
,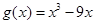 ,
,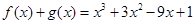
令 ,则
,则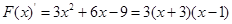 ,令
,令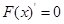 ,
, ∴
∴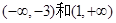 为单调递增区间,
为单调递增区间,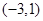 为单调递减区间,其中F(-3)=28为极大值,所以如果区间[k,2]最大值为28,即区间包含极大值点
为单调递减区间,其中F(-3)=28为极大值,所以如果区间[k,2]最大值为28,即区间包含极大值点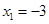 ,所以
,所以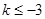
【考点定位】此题应该说是导数题目中较为常规的类型题目,考查的切线,单调性,极值以及最值问题都是课本中要求的重点内容,也是学生掌握比较好的知识点,在题目中能够发现F(-3)=28,和分析出区间[k,2]包含极大值点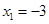 ,比较重要
,比较重要
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com