
题目列表(包括答案和解析)
如图,在四棱锥 中,
中, ⊥底面
⊥底面 ,底面
,底面 为正方形,
为正方形, ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点.
(I)求证: 平面
平面 ;
;
(II)求证: ;
;
(III)设PD=AD=a, 求三棱锥B-EFC的体积.

【解析】第一问利用线面平行的判定定理, ,得到
,得到
第二问中,利用
 ,所以
,所以
又因为 ,
, ,从而得
,从而得
第三问中,借助于等体积法来求解三棱锥B-EFC的体积.
(Ⅰ)证明:
 分别是
分别是 的中点,
的中点, 
 ,
, . …4分
. …4分
(Ⅱ)证明: 四边形
四边形 为正方形,
为正方形, .
.
 ,
,  .
.
 ,
,  ,
,
 .
. ,
, . ………8分
. ………8分
(Ⅲ)解:连接AC,DB相交于O,连接OF, 则OF⊥面ABCD,
∴

某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验如下:
|
零件的个数 |
2 |
3 |
4 |
5 |
|
加工的时间 |
2.5 |
3 |
4 |
4.5 |
(1)在给定坐标系中画出表中数据的散点图;
(2)求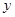 关于
关于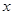 的线性回归方程
的线性回归方程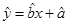 ;
;
(3)试预测加工10个零件需要多少时间?
(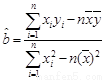 ,
,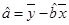 )
)
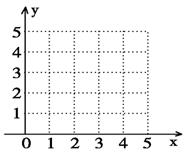
【解析】第一问中,利用表格中的数据先作出散点图
第二问中,求解均值a,b的值,从而得到线性回归方程。
第三问,利用回归方程将x=10代入方程中,得到y的预测值。
解:(1)散点图(略) (2分)
(2)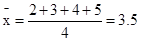
 (4分)
(4分)

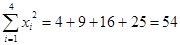 ∴
∴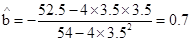 (7分)
(7分)
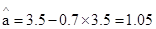 (8分)∴回归直线方程:
(8分)∴回归直线方程: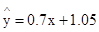 (9分)
(9分)
(3)当 ∴预测加工10个零件需要8.05小时。
∴预测加工10个零件需要8.05小时。
已知函数
(1)若函数 的图象经过P(3,4)点,求a的值;
的图象经过P(3,4)点,求a的值;
(2)比较 大小,并写出比较过程;
大小,并写出比较过程;
(3)若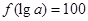 ,求a的值.
,求a的值.
【解析】本试题主要考查了指数函数的性质的运用。第一问中,因为函数 的图象经过P(3,4)点,所以
的图象经过P(3,4)点,所以 ,解得
,解得 ,因为
,因为 ,所以
,所以 .
.
(2)问中,对底数a进行分类讨论,利用单调性求解得到。
(3)中,由 知,
知, .,指对数互化得到
.,指对数互化得到 ,,所以
,,所以 ,解得所以,
,解得所以, 或
或  .
.
解:⑴∵函数 的图象经过
的图象经过 ∴
∴ ,即
,即 . … 2分
. … 2分
又 ,所以
,所以 .
………… 4分
.
………… 4分
⑵当 时,
时, ;
;
当 时,
时, . ……………… 6分
. ……………… 6分
因为, ,
,
当 时,
时, 在
在 上为增函数,∵
上为增函数,∵ ,∴
,∴ .
.
即 .当
.当 时,
时, 在
在 上为减函数,
上为减函数,
∵ ,∴
,∴ .即
.即 . …………………… 8分
. …………………… 8分
⑶由 知,
知, .所以,
.所以, (或
(或 ).
).
∴ .∴
.∴ , … 10分
, … 10分
∴ 或
或
 ,所以,
,所以, 或
或  .
.
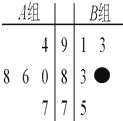 某校团委会组织该校高中一年级某班以小组为单位利用周末时间进行了一次社会实践活动,且每个小组有5名同学,在实践活动结束后,学校团委会对该班的所有同学都进行了测评,该班的A、B两个小组所有同学所得分数(百分制)的茎叶图如左侧图所示,其中B组一同学的分数已被污损,但知道B组学生的平均分比A组学生的平均分高1分.
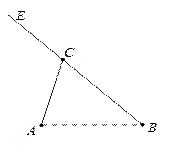
某校团委会组织该校高中一年级某班以小组为单位利用周末时间进行了一次社会实践活动,且每个小组有5名同学,在实践活动结束后,学校团委会对该班的所有同学都进行了测评,该班的A、B两个小组所有同学所得分数(百分制)的茎叶图如左侧图所示,其中B组一同学的分数已被污损,但知道B组学生的平均分比A组学生的平均分高1分.(本小题满分12分) 如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120 km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车 站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
(1)计算A,C两站距 离,及B,C两站距离;(2)若甲、乙两车上各有一名旅客需要交换到对方汽车上,问能否在车站C处利用停留时间交换.(3)求10点时甲、乙两车的距离.(可能用到的参考数据:
离,及B,C两站距离;(2)若甲、乙两车上各有一名旅客需要交换到对方汽车上,问能否在车站C处利用停留时间交换.(3)求10点时甲、乙两车的距离.(可能用到的参考数据: ,
, ,
, ,
, )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com