(2010?徐汇区一模)在研究摩擦力特点的实验中,将木块放在水平长木板上,如图(a)所示,用力沿水平方向拉木块,拉力从零开始逐渐增大.分别用力传感器采集拉力和木块所受到的摩擦力,并用计算机绘制出摩擦力F
f随拉力F的变化图象,如图(b)所示.已知木块质量为0.78kg,重力加速度g=10m/s
2,sin37°=0.60,cos37°=0.80.
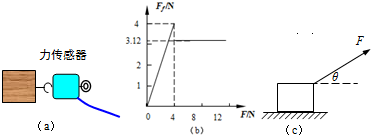
(1)求木块与长木板间的动摩擦因数;
(2)如图(c),若木块在与水平方向成37°角斜向右上方的恒定拉力F作用下,以a=2m/s
2的加速度从静止开始沿水平面做匀变速直线运动,拉力大小应为多大?
(3)在(2)中力作用2s后撤去拉力F,再经过多少时间木块停下?整个运动过程中摩擦力对木块做了多少功?

