
题目列表(包括答案和解析)
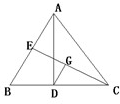 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
|
| ||
| 2 |
| ||
| 2 |

 选考题
选考题| 1 | ||
|
|
| π |
| 3 |
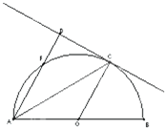 选做题:请考生从22、23、24题中任选一题作答,并在答题卡上把所选题目的题号用2B铅笔涂黑.注意所做题目的题号必须与所涂的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.
选做题:请考生从22、23、24题中任选一题作答,并在答题卡上把所选题目的题号用2B铅笔涂黑.注意所做题目的题号必须与所涂的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.| 甲组 | 乙组 | ||||
| 9 | 9 | 0 | X | 8 | 9 |
| 1 | 1 | 1 | 0 | ||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com