
题目列表(包括答案和解析)
(本题满分12分) 商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少。把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元。现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的相同价格(标价)出售. 问:
(Ⅰ)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(Ⅱ)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
(本题满分12分)
用铁皮制作一个无盖的圆锥形容器,如图,已知该圆锥的母线与底面所在平面的夹角为 ,容器的高为
,容器的高为 .制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到
.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到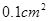 )
)

(本题满分12分)
 某校高二(17)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
某校高二(17)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:


(1)求全班人数;
(2)求分数在 之间的人数;并计算频率分布直方图中
之间的人数;并计算频率分布直方图中 间的矩形的高;
间的矩形的高;
(3)若要从分数在 之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在
之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在 之间的概率.
之间的概率.
(本题满分12分)
把边长为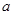 的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为
的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为 ,容积为
,容积为 .
.

(Ⅰ)写出函数 的解析式,并求出函数的定义域;
的解析式,并求出函数的定义域;
(Ⅱ)求当x为多少时,容器的容积最大?并求出最大容积.
(本题满分12分) 若三角形的一个顶点为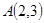 ,两条高所在的直线方程
,两条高所在的直线方程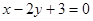 和
和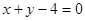 ,试求此三角形三边所在的直线方程;
,试求此三角形三边所在的直线方程;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com