题目列表(包括答案和解析)
如图所示，平面坐标系Oxy中，在y＞0的区域存在沿y轴负方向的匀强电场，场强大小为E，在－h＜y＜0的区域Ⅰ中存在垂直纸面向外的匀强磁场，磁感应强度大小为B，在y＜－h的区域Ⅱ中存在垂直纸面向里的匀强磁场，磁感应强度大小为2B．A是y轴上的一点， C是x轴上的一点．一质量为m、电荷量为q的带正电的粒子以某一初速度沿x轴正方向从A点进入电场区域，继而通过C点以速度方向与x轴夹角为φ＝30°进入磁场区域Ⅰ，并以垂直边界y＝－h的速度进入磁场区域Ⅱ．粒子重力不计．试求：（1）粒子经过C点时的速度大小v；
（2）A、C两点与O点间的距离y0、x0；
（3）粒子从A点出发，经过多长时间可回到y＝y0处？
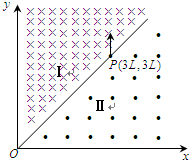如图所示，在空间中有一坐标系oxy，其第一象限中充满着两个方向不同的匀强磁场区域Ⅰ和Ⅱ．直线OP是它们的边界．区域Ⅰ中的磁感应强度为2B，方向垂直纸面向内，区域Ⅱ中的磁感应强度为B，方向垂直纸面向外，边界上的P点坐标为（3L，3L）．一质量为m，电荷量为+q的粒子从P点平行于y轴正方向以速度v0=| 2BqL | m |
| 2BqL |
| m |
一、1、BC 2、ACD 3、BD 4、A 5、ACD 6、ABC 7、BD 8、B
二、实验题：（18分）将答案填在题目的空白处，或者要画图连线。
9、（6分）（1）
10、（12分）
①（4分）
②串（2分） 290Ω（3分）．③偏大（3分）
三、本大题共三小题共计54分．解答时请写出必要的文字说明、方程式和重要的演算步骤．只写出最后答案的不能得分．有数值计算的题．答案中必须明确写出数值和单位
11、（16分）设A的质量为m，A静止，有：
①……1分
设B的质量为mB，B与A碰前速度为v1，由机械能守恒定律可知：
②……1分
B与A发生完全弹性碰撞，设碰后A、B速度大小分别为
，有：
③……2分
④……2分
可得：
⑤……1分
B反弹，机械能守恒：
⑥……1分
由②――⑥可知：
⑦……1分
由题可知：
⑧……1分
设C与A碰前速度为v2，由机械能守恒定律可知：
⑨……1分
C与A碰，碰后速度为v3，由动量守恒：
⑩……1分
A、 C分离发生在弹簧原长处O，不分离即系统至O点速度为零。由系统机械能守恒可知：
11……2分
解得：
12……2分
12、（18分）⑴PQ在区域Ⅱ中距中间边界
，而MN在区域I 距中间边界
时，PQ边产生的感应电动势
（2分）
MN边产生的感应电动势
（2分）
故回路中的电动势
V (2分）
由于线框匀速运动，故水平拉力做的功等于线框中产生的焦耳热，即
(2分）
⑵设初速度为
，匀速运动一段时间后减速，MN边到达中间界线时速度为
，接着又匀速运动一段时间后，再减速，最后速度为0，则对跨越中间边界的过程据动量定理有
(2分）
对跨越最右边界的过程据动量定理有
(2分）
线圈运动时产生的平均感应电动势
，电量
联立化简得
（1分）
由上式可得：
(1分）
则
(1分)
故
(l分)
(1分)
则
(1分)
13、（20分）（1）由题可知粒子在磁场Ⅰ中圆运动的圆心角为60°，相应圆运动半径为：
①…… 1分
由
②……1分
可知
③……1分
④……2分
（2）粒子在电场中做类平抛运动，有：
⑤……1分
⑥……1分
⑦……1分
可知：
⑧……1分
⑨……2分 
⑩……2分
（3）根据运动对称性可知：
第一次返回y=y0前在磁场Ⅰ中运动的总时间
11……1分
在磁场Ⅱ中运动的总时间
12……2分
故第一次返回y=y0前运动的总时间
13……2分
之后运动呈周期性，故返回y=y0前运动的总时间
14……2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com