
题目列表(包括答案和解析)
 满足:
满足: b∈G,
b∈G,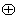 e=e
e=e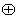 a=a,则称G关于运算
a=a,则称G关于运算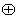 为“融洽集”。
为“融洽集”。 为整数的加法;
为整数的加法; 为整数的乘法;
为整数的乘法;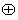 为平面向量的加法;
为平面向量的加法; 为多项式的加法;
为多项式的加法;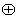 为复数的乘法。
为复数的乘法。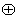 为“融洽集”的是( )。(写出所有“融洽集”的序号)
为“融洽集”的是( )。(写出所有“融洽集”的序号)(08年大连市一模理) 若在二项式![]() 的展开式中任取一项,该项的系数为奇数的概率是1,则在二项式
的展开式中任取一项,该项的系数为奇数的概率是1,则在二项式![]() 的展开式中任取一项,该项的系数为奇数的概率是p,为偶数的概率是q,那么p―q= 。
的展开式中任取一项,该项的系数为奇数的概率是p,为偶数的概率是q,那么p―q= 。
已知二次函数f(x)=ax2+bx+c(a≠0),有关叙述
(1)值域为R;
(2)在(-∞,-![]() 】上单调递减,在【-
】上单调递减,在【-![]() ,+∞)上单调递增;
,+∞)上单调递增;
(3)只有当b=0时,函数才是偶函数;
(4)若f(x1)=f(x2)=0,则有f(x1+x2)=c.把正确的序号全部写在______内。
非空集合M关于运算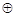 满足:(1)对任意的a,
满足:(1)对任意的a,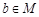 ,都有
,都有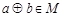 ;(2)存在
;(2)存在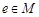 ,使得对一切
,使得对一切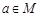 ,都有
,都有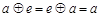 ,则称M关于运算
,则称M关于运算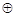 为“理想集”。
为“理想集”。
现给出下列集合与运算:
①M={非负整数},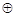 为整数的加法;②M={偶数},
为整数的加法;②M={偶数},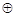 为整数的乘法;
为整数的乘法;
③M={二次三项式},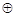 为多项式的加法;④M={平面向量},
为多项式的加法;④M={平面向量},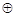 为平面向量的加法;
为平面向量的加法;
其中M关于运算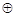 为“理想集”的是
。(只需填出相应的序号)
为“理想集”的是
。(只需填出相应的序号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com