（本小题满分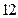分）某学校高三年级有学生1000名，经调查研究,其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼(称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学.
(Ⅰ)求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
(Ⅱ) 测得该年级所抽查的100名同学身高(单位：厘米) 频率分布直方图如右图：
(ⅰ) 统计方法中，同一组数据常用该组区间的中点值（例如区间的中点值为165）作为代表．据此，计算这100名学生身高数据的期望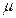及标准差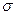(精确到0.1)；
(ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在范围中的学生的人数．
(Ⅲ) 如果以身高达170cm作为达标的标准，对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表

	身高达标	身高不达标	总计
积极参加体育锻炼	40
不积极参加体育锻炼		15
总计			100

(ⅰ)完成上表；
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
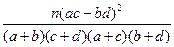参考公式:K=,参考数据:

P(Kk)	0.40	0.25	0.15	0.10	0.05	0.025
k	0.708	1.323	2.072	2.706	3.841	5.024

某学校高三年级有学生1000名，经调查研究，其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼（称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学．
（Ⅰ）求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
（Ⅱ）测得该年级所抽查的100名同学身高（单位：厘米）频率分布直方图如右图：
（ⅰ）统计方法中，同一组数据常用该组区间的中点值（例如区间[160，170）的中点值为165）作为代表．据此，计算这100名学生身高数据的期望μ及标准差φ（精确到0.1）；
（ⅱ）若总体服从正态分布，以样本估计总体，据此，估计该年级身高在（158.6，181.4）范围中的学生的人数．
（Ⅲ）如果以身高达170cm作为达标的标准，对抽取的100名学生，得到下列联表：
体育锻炼与身高达标2×2列联表

	身高达标	身高不达标	总计
积极参加体育锻炼	40
不积极参加体育锻炼		15
总计			100

（ⅰ）完成上表；
（ⅱ）请问有多大的把握认为体育锻炼与身高达标有关系？
参考公式：K²=

π(ac-bd)2

(a+b)(c+d)(a+c)(b+d)

，参考数据：

P（K2≥k）	0.40	0.25	0.15	0.10	0.05	0.025
k	0.708	1.323	2.072	2.706	3.841	5.024

为了解高中一年级学生身高情况，某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查，测得身高频数分布表如下表1、表2．

表1：男生身高频数分布表

 

身高（cm）	[160，165）	[165，170）	[170，175）	[175，180）	[180，185）	[185，190）
频数	2	5	14	13	4	2

 

表2：女生身高频数分布表

 

身高（cm）	[150，155）	[155，160）	[160，165）	[165，170）	[170，175）	[175，180）
频数	1	7	12	6	3	1

 

（I）求该校男生的人数并完成下面频率分布直方图；

（II）估计该校学生身高在的概率；

（III）从样本中身高在180190cm之间的男生中任选2人，求至少有1人身高在185190cm之间的概率。

【解析】第一问样本中男生人数为40 ，

由分层抽样比例为10%可得全校男生人数为400

（2）中由表1、表2知，样本中身高在的学生人数为：5+14+13+6+3+1=42，样本容量为70 ，所以样本中学生身高在的频率 

故由估计该校学生身高在的概率 

（3）中样本中身高在180185cm之间的男生有4人，设其编号为①②③④ 样本中身高在185190cm之间的男生有2人，设其编号为⑤⑥从上述6人中任取2人的树状图，故从样本中身高在180190cm之间的男生中任选2人得所有可能结果数为15，求至少有1人身高在185190cm之间的可能结果数为9，因此，所求概率

由表1、表2知，样本中身高在的学生人数为：5+14+13+6+3+1=42，样本容量为70 ，所以样本中学生身高在

的频率-----------------------------------------6分

故由估计该校学生身高在的概率．--------------------8分

（3）样本中身高在180185cm之间的男生有4人，设其编号为①②③④ 样本中身高在185190cm之间的男生有2人，设其编号为⑤⑥从上述6人中任取2人的树状图为：

--10分

故从样本中身高在180190cm之间的男生中任选2人得所有可能结果数为15，求至少有1人身高在185190cm之间的可能结果数为9，因此，所求概率

 

(10分)为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测

试，将所得数据整理后，画出了频率分布直方图(如上图)，图中从左到右各小长方形面积之

比为2：4：17：15：9：3，第二小组频数为12.

（1）第二小组的频率是多少？样本容量是多少？

（2）若次数在110以上（含110次）为达标，试估计该学校全体高一学生的达标率是多少？