(12分)如图所示，MM′，NN′为相距L＝30cm的光滑平行金属导轨，导轨左端接有定值电阻R＝0.1Ω，金属导体棒ab垂直导轨放在导轨上，金属棒的电阻R_0­＝0.3Ω,导体棒可贴着导轨无摩擦滑动，导轨电阻不计。导轨右端接一水平放置的平行板电容器，两水平金属板间的距离为d＝27cm，整个装置都放在垂直纸面向里的匀强磁场中。当ab以速度v向右匀速运动时，一带电微粒刚好能以速率v在平行金属板间作半径为r＝m的匀速圆周运动。（g＝10m/s²）求：

（l）为使带电微粒做上述要求的运动，v应为多少？

（2）若匀强磁场的磁感应强度B＝2.0T，则此时作用在ab棒上的水平拉力应为多少？

(12分)如图所示，匀强电场的电场强度E = 4V/m，方向水平向左。匀强磁场的磁感应强度B =2T，垂直纸面向里。质量m =1g的带正电小物块A，从M点沿绝缘粗糙的竖直壁无初速度下滑，它滑行0.8m到N点时就离开壁做曲线运动，在P点物块A瞬时受力平衡，此时其速度与水平方向成45°角。设P与M的高度差为1.6m。（g取10m/s²）求：

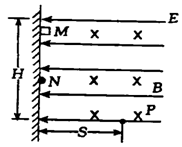
（1）A沿壁下滑时摩擦力做的功？

（2）P与M水平距离？

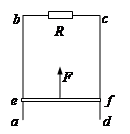
(12分)如图所示，足够长的光滑导轨ab、cd固定在竖直平面内，导轨间距为l，b、c两点间接一阻值为R的电阻。ef是一水平放置的导体杆，其质量为m、有效电阻值为R，杆与ab、cd保持良好接触。整个装置放在磁感应强度大小为B的匀强磁场中，磁场方向与导轨平面垂直。现用一竖直向上的力拉导体杆，使导体杆从静止开始做加速度为的匀加速运动，g为重力加速度，不计导轨电阻及感应电流间的相互作用。求：

⑴导体杆上升h高度的过程中通过电阻的电量；

⑵设导体杆从=0时刻由静止开始运动，试推导出导体杆所受拉力随时间变化的关系式。

(12分)如图所示，倾角θ=30°、宽度L="1" m的足够长的U形平行光滑金属导轨，固定在磁感应强度B="1" T、范围充分大的匀强磁场中，磁场方向与导轨平面垂直。用平行于导轨、功率恒为6 W的牵引力F牵引一根质量为m="0.2" kg、电阻R="1" Ω的放在导轨上的金属棒ab，由静止开始沿导轨向上移动(ab始终与导轨接触良好且垂直)。当ab棒移动2.8 m时，获得稳定速度，在此过程中，克服安培力做功为5.8 J(不计导轨电阻及一切摩擦，g取10 m/s²)，求：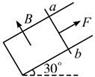

(1)ab棒的稳定速度。
(2)ab棒从静止开始达到稳定速度所需时间。

(12分)如图所示，在直角坐标系的第二象限和第四象限中的直角三角形区域内，分布着磁感应强度均为B=5.0×10^-3T的匀强磁场，方向分别垂直纸面向外和向里。一质量m=6.4×10^-27kg、电荷量q=+3.2×10^-19C的带电粒子（带电粒子重力不计），由静止开始经加速电压U=1250V的电场（图中未画出）加速后，从坐标点M（-4,）m处平行于x轴向右运动，并先后通过两个匀强磁场区域。

（1）求带电粒子在磁场中的运动半径；（结果保留根号）
（2）在图中画出从直线x=-4m到直线x=4m之间带电粒子的运动轨迹；
（3）求出带电粒子在两个磁场区域偏转所用的时间。