
题目列表(包括答案和解析)
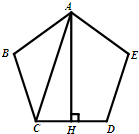 如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得AC=
如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得AC=| 8-8cos108° |
| 1 |
| cos72° |
小明和同桌小聪一起合作探索:如图,一架5米长的梯子AB斜靠在铅直的墙壁AC上,这时梯子的底端B到墙角C的距离为1.4米.如果梯子的顶端A沿墙壁下滑0.8米,那么底端B将向左移动多少米?

(1)小明的思路如下,请你将小明的解答补充完整:
解:设点B将向左移动x米,即BE=x,则:
EC=
x+1.4,DC=AC-DC= -0.8=4,
-0.8=4,
而DE=5,在Rt△DEC中,由EC2+DC2=DE2,
得方程为: , 解方程得: ,
∴点B将向左移动 米.
(2)解题回顾时,小聪提出了如下两个问题:
①将原题中的“下滑0.8米”改为“下滑1.8米”,那么答案会是1.8米吗?为什么?
②梯子顶端下滑的距离与梯子底端向左移动的距离能相等吗?为什么?
请你解答小聪提出的这两个问题.
 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得 ,据此可得cos72°的值所在区间为( )
,据此可得cos72°的值所在区间为( )
 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得 ,据此可得cos72°的值所在区间为( )
,据此可得cos72°的值所在区间为( )
 如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得
如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得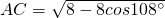 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得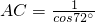 ,据此可得cos72°的值所在区间为
,据此可得cos72°的值所在区间为湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com