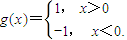已知函数f（x）=x²+m，其中m∈R，定义数列{a_n}如下：a₁=0，a_n+1=f（a_n），n∈N*．
（1）当m=1时，求a₂，a₃，a₄的值；
（2）是否存在实数m，使a₂，a₃，a₄成等比数列？若存在，请求出实数m的值，并求出等比数列的公比；若不存在，请说明理由．
（3）设m=-1，f^-1（x）为f（x）在x∈[0，+∞）的反函数，数列{b_n}满足：b₁=1，b_n+1=f^-1（b_n²）（n∈N*），记S_n=b₁²+b₂²+…+b_n²，求使S_n＞2010成立的最小正整数n的值．

已知函数f（x）=x²+m，其中m∈R，定义数列{a_n}如下：a₁=0，a_n+1=f（a_n），n∈N*．
（1）当m=1时，求a₂，a₃，a₄的值；
（2）是否存在实数m，使a₂，a₃，a₄成等比数列？若存在，请求出实数m的值，并求出等比数列的公比；若不存在，请说明理由．
（3）设m=-1，f^-1（x）为f（x）在x∈[0，+∞）的反函数，数列{b_n}满足：b₁=1，b_n+1=f^-1（b_n²）（n∈N*），记S_n=b₁²+b₂²+…+b_n²，求使S_n＞2010成立的最小正整数n的值．

已知集合S_n={（x₁，x₂，…，x_n）|x₁，x₂，…，x_n是正整数1，2，3，…，n的一个排列}（n≥2），函数
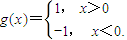
对于（a₁，a₂，…a_n）∈S_n，定义：b_i=g（a_i-a₁）+g（a_i-a₂）+…+g（a_i-a_i-1），i∈{2，3，…，n}，b₁=0，称b_i为a_i的满意指数．排列b₁，b₂，…，b_n为排列a₁，a₂，…，a_n的生成列．
（Ⅰ）当n=6时，写出排列3，5，1，4，6，2的生成列；
（Ⅱ）证明：若a₁，a₂，…，a_n和a'₁，a'₂，…，a'_n为S_n中两个不同排列，则它们的生成列也不同；
（Ⅲ）对于S_n中的排列a₁，a₂，…，a_n，进行如下操作：将排列a₁，a₂，…，a_n从左至右第一个满意指数为负数的项调至首项，其它各项顺序不变，得到一个新的排列．证明：新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加2．