
题目列表(包括答案和解析)
在棱长为 的正方体
的正方体 中,
中, 是线段
是线段 的中点,
的中点, .
.
(1) 求证: ^
^ ;
;
(2) 求证: //平面
//平面 ;
;
(3) 求三棱锥 的表面积.
的表面积.

【解析】本试题考查了线线垂直和线面平行的判定定理和表面积公式的运用。第一问中,利用 ,得到结论,第二问中,先判定
,得到结论,第二问中,先判定 为平行四边形,然后
为平行四边形,然后 ,可知结论成立。
,可知结论成立。
第三问中, 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
,
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为 .
.
解: (1)证明:根据正方体的性质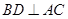 ,
,
因为 ,
,
所以 ,又
,又 ,所以
,所以 ,
, ,
,
所以 ^
^ .
………………4分
.
………………4分
(2)证明:连接 ,因为
,因为 ,
,
所以 为平行四边形,因此
为平行四边形,因此 ,
,
由于 是线段
是线段 的中点,所以
的中点,所以 , …………6分
, …………6分
因为
 面
面 ,
,
 平面
平面 ,所以
,所以 ∥平面
∥平面 . ……………8分
. ……………8分
(3) 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
……………………10分
,
……………………10分
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为

已知数列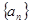 满足
满足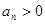 且对一切
且对一切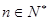 ,
,
有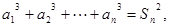
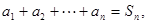
(Ⅰ)求证:对一切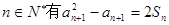
(Ⅱ)求数列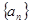 通项公式.
通项公式.
(Ⅲ)求证: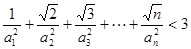
【解析】第一问利用,已知表达式,可以得到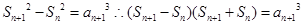 ,然后得到
,然后得到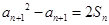 ,从而求证
。
,从而求证
。
第二问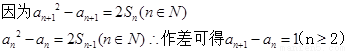 ,可得数列的通项公式。
,可得数列的通项公式。
第三问中,利用放缩法的思想,我们可以得到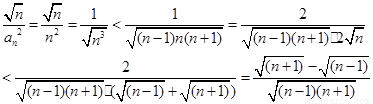
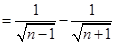 然后利用累加法思想求证得到证明。
然后利用累加法思想求证得到证明。
解: (1) 证明:
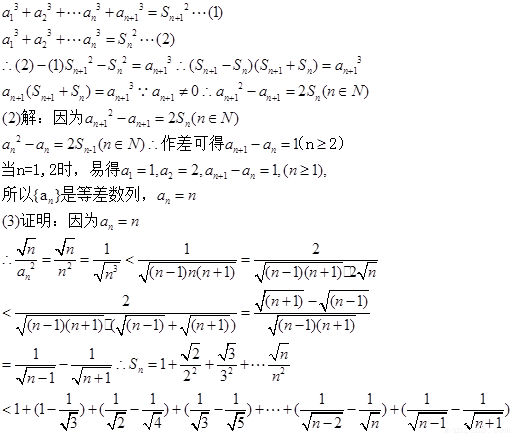
已知函数 ,数列
,数列 的项满足:
的项满足: ,(1)试求
,(1)试求
(2) 猜想数列 的通项,并利用数学归纳法证明.
的通项,并利用数学归纳法证明.
【解析】第一问中,利用递推关系 ,
, 
 ,
, 
第二问中,由(1)猜想得: 然后再用数学归纳法分为两步骤证明即可。
然后再用数学归纳法分为两步骤证明即可。
解: (1)  ,
,

 ,
,  …………….7分
…………….7分
(2)由(1)猜想得:
(数学归纳法证明)i)  ,
,
 ,命题成立
,命题成立
ii) 假设 时,
时, 成立
成立
则 时,
时,


综合i),ii) :  成立
成立
已知函数 , 其中
, 其中 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,求曲线
时,求曲线 的单调区间与极值.
的单调区间与极值.
【解析】第一问中利用当 时,
时, ,
,
 ,得到切线方程
,得到切线方程
第二问中,

对a分情况讨论,确定单调性和极值问题。
解: (1) 当 时,
时, ,
,
 ………………………….2分
………………………….2分

 切线方程为:
切线方程为:  …………………………..5分
…………………………..5分
(2) 
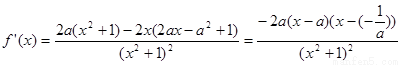 …….7
…….7 分
分
分类: 当 时, 很显然
时, 很显然
 的单调增区间为:
的单调增区间为:  单调减区间:
单调减区间:  ,
,
 ,
,  ………… 11分
………… 11分
当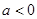 时
时 的单调减区间:
的单调减区间:  单调增区间:
单调增区间: 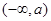 ,
,

 ,
, 
(1)求f(x)的表达式;
(2)设x1=2,xn=f(xn-1)(n=2,3,…),求证:数列{![]() }成等差数列;
}成等差数列;
(3)在条件(2)下,求{xn}的通项公式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com