
题目列表(包括答案和解析)
设 .
.
(1)若函数 在区间
在区间 内单调递减,求
内单调递减,求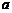 的取值范围;
的取值范围;
(2)若函数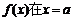 处取得极小值是
处取得极小值是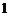 ,求
,求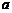 的值,并说明在区间
的值,并说明在区间 内函数
内函数 的单调性.
的单调性.
已知函数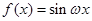
 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减;如图,四边形
上单调递减;如图,四边形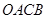 中,
中,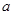 ,
, ,
, 为
为 的内角
的内角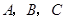 的对边,
的对边,
且满足 .
.

(Ⅰ)证明: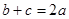 ;
;
(Ⅱ)若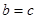 ,设
,设 ,
,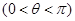 ,
,
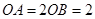 ,求四边形
,求四边形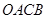 面积的最大值.
面积的最大值.
已知函数
 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减;如图,四边形
上单调递减;如图,四边形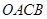 中,
中,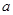 ,
,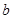 ,
, 为
为 的内角
的内角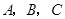 的对边,
的对边,
且满足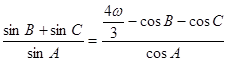 .
.
(Ⅰ)证明: ;
;
(Ⅱ)若 ,设
,设 ,
,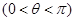 ,
,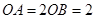 ,求四边形
,求四边形 面积的最大值.
面积的最大值.

 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减;如图,四边形
上单调递减;如图,四边形 中,
中, ,
, ,
, 为
为 的内角
的内角 的对边,
的对边, .
.
 ;
; ,设
,设 ,
, ,
, ,求四边形
,求四边形 面积的最大值.
面积的最大值.(13分)
设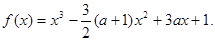
(I)若函数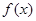 在区间(1,4)内单调递减,求a的取值范围;
在区间(1,4)内单调递减,求a的取值范围;
(II)若函数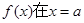 处取得极小值是1,求a的值,并说明在区间(1,4)内函数
处取得极小值是1,求a的值,并说明在区间(1,4)内函数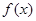 的单调性.
的单调性.
一、选择题:本大题共12小题,每小题5分,共60分。
AABC BDDC DBAB
二、填空题:本大题共4小题,每小题4分,共16分。
13.3 14.2 15..files/image230.gif) 16.①④
16.①④
三、解答题:本大题共6小题,共74分。
17.解:.files/image232.gif) 1分
1分
∵.files/image234.gif) ∴CD⊥AB,∴∠ADC=900。
∴CD⊥AB,∴∠ADC=900。
在Rt.files/image115.gif) 中,
中,.files/image237.gif) 4分
4分
.files/image239.gif) 6分
6分
.files/image241.gif) ∴
∴.files/image243.gif) 7分
7分
又∵.files/image245.gif) ,∴
,∴.files/image247.gif) 9分
9分
∴.files/image249.gif) =
=.files/image251.gif) ×
×.files/image253.gif) -
-.files/image255.gif) ×
×.files/image257.gif) 12分
12分
18.解:(Ⅰ)当.files/image259.gif) 时,
时,.files/image261.gif) 1分
1分
当.files/image054.gif) ≥2时,
≥2时,
.files/image264.gif) 3分
3分
∵.files/image266.gif) 是等差数列,
是等差数列,.files/image268.gif) 符合
符合.files/image054.gif) ≥2时,
≥2时,.files/image270.gif) 的形式,
的形式,
∴.files/image272.gif) ∴
∴.files/image274.gif) 5分
5分
(Ⅱ)∵.files/image276.gif) ,由题意得
,由题意得.files/image278.gif) 7分
7分
又.files/image280.gif) ,解得
,解得.files/image282.gif) 8分
8分
∴.files/image284.gif) 9分
9分
由.files/image286.gif) 。
。
∴.files/image288.gif) ,即
,即.files/image290.gif) 是首项为2,
是首项为2,
公比为16的等比数列 11分
∴数列.files/image290.gif) 的前n项和
的前n项和.files/image292.gif) 12分
12分
19.解:设90-140分之间的人数是.files/image054.gif) ,由130-140分数段的人数为2人
,由130-140分数段的人数为2人
可知0.005×10×.files/image054.gif) =2,得
=2,得.files/image295.gif)
(Ⅰ)平均数.files/image297.gif) 95×0.1+105×0.25+115×0.45+125×0.15+135×0.05=113. 4分
95×0.1+105×0.25+115×0.45+125×0.15+135×0.05=113. 4分
中位数.files/image299.gif) =
=.files/image301.gif) 6分
6分
(Ⅱ)依题意,第一组共有40×0.01×10=4人,记作.files/image303.gif) ;第五组共有2分,记作
;第五组共有2分,记作.files/image305.gif) 从第一组和第五组中任意选出两人共有下列15种选法:{A1,A2}、{A1,A3}、{A1,A4}、{A2,A3}、{A2,A4}、{A3,A4};{A1,B1}、{A2,B1}、{A2,B2}、
从第一组和第五组中任意选出两人共有下列15种选法:{A1,A2}、{A1,A3}、{A1,A4}、{A2,A3}、{A2,A4}、{A3,A4};{A1,B1}、{A2,B1}、{A2,B2}、
{A3,B1}、{A3,B2}、{A4,B1}、{A4,B2}、{A1,B2}、 9分
设事件A:选出的两人为“黄金搭档组”。若两人成绩之差大于20,则两人分别来自于第一组和第五组,共有8中选法,故.files/image307.gif) 12分
12分
20.解:(Ⅰ)空间几何体的直观图如图所示,
.files/image309.jpg) 且可得到平面ABCD⊥平面ABG,四边形
且可得到平面ABCD⊥平面ABG,四边形
ABCD为正方形,AG=BG=.files/image311.gif) ,
,
故AG⊥BG………………………………4分
(Ⅱ)∵平面ABCD⊥平面ABG,
面ABCD∩平面ABG=AB,CB⊥AB,
∴CB⊥平面ABG,故CB⊥AG………6分
又AG⊥BG,∴AG⊥平面BGC。
∴平面AGD⊥平面BGC………………8分
(Ⅲ)过G作GE⊥AB,垂足为E,则GE⊥平面ABCD
.files/image313.gif) 12分
12分
21.(Ⅰ)依题意,直线.files/image315.gif) 显然不平行于坐标轴,故
显然不平行于坐标轴,故.files/image317.gif) 可化为
可化为.files/image319.gif)
将 .files/image319.gif) 代入
代入.files/image212.gif) ,消去
,消去.files/image083.gif) ,得
,得
.files/image324.gif) ① 1分
① 1分
由直线.files/image315.gif) 与椭圆相交于两个不同的点,得
与椭圆相交于两个不同的点,得
△=.files/image326.gif) 2分
2分
化简整理即得.files/image328.gif) (☆) 4分
(☆) 4分
(Ⅱ)A(x1,y1),B(x2,y2),由①,得.files/image330.gif) ② 5分
② 5分
因为.files/image332.gif) ,
,
得.files/image334.gif) ③ 6分
③ 6分
由②③联立,解得.files/image336.gif) ④ 7分
④ 7分
△OAB的面积.files/image338.gif)
=.files/image340.gif)
上式取等号的条件是.files/image342.gif) ,
,
即.files/image344.gif) ………………9分
………………9分
当.files/image346.gif) 时,由④解得
时,由④解得.files/image348.gif) ;当
;当.files/image350.gif) 时,由④解得
时,由④解得.files/image352.gif) 。
。
将.files/image354.gif) 及
及.files/image356.gif) 这两组值分别代入①,
这两组值分别代入①,
均可解出.files/image358.gif) 11分
11分
经验证,.files/image358.gif) ,
,.files/image344.gif) 满足(☆)式。
满足(☆)式。
所以,△OAB的面积取得最大值时椭圆方程是.files/image362.gif) 12分
12分
注:若未验证(说明.files/image364.gif) )满足(☆)式,扣1分。
)满足(☆)式,扣1分。
22.(Ⅰ)由题设条件,可设.files/image366.gif) 这里
这里.files/image368.gif) 1分
1分
所以.files/image370.gif) ①
①
又.files/image372.gif) 有两个相等的实数根,而
有两个相等的实数根,而.files/image374.gif) ,
,
所以判别式△=.files/image376.gif) ,即
,即.files/image378.gif) 3分
3分
解得.files/image380.gif) (舍去),或
(舍去),或.files/image382.gif) =-1,代入①式得
=-1,代入①式得.files/image384.gif) 4分
4分
(Ⅱ).files/image386.gif)
因为.files/image388.gif) 在区间
在区间.files/image390.gif) 内单调递减,
内单调递减,
所以.files/image392.gif) 当
当.files/image394.gif) 时恒成立 5分
时恒成立 5分
∵.files/image368.gif) ,对称轴为直线
,对称轴为直线.files/image397.gif) 在
在.files/image390.gif) 上为增函数,
上为增函数,
故只需.files/image400.gif) 8分
8分
注意到.files/image368.gif) ,解得
,解得.files/image403.gif) (舍去)。故
(舍去)。故.files/image382.gif) 的取值范围是
的取值范围是.files/image405.gif) 10分
10分
(Ⅲ)当.files/image407.gif) 时,方程
时,方程.files/image228.gif) 即为
即为.files/image410.gif)
令.files/image412.gif) 由
由.files/image414.gif) ,得
,得.files/image416.gif) …11分
…11分
易知.files/image418.gif) 在
在.files/image420.gif) 和
和.files/image422.gif) 上单调递增,在
上单调递增,在.files/image424.gif) 上单调递减,
上单调递减,
.files/image418.gif) 的极大值
的极大值.files/image426.gif) 的极小值
的极小值.files/image428.gif) 13分
13分
而.files/image430.gif) 使,
使,.files/image432.gif) 时,
时,.files/image434.gif) ,
,
故函数.files/image418.gif) 的图象与
的图象与.files/image083.gif) 轴有且只有一个公共点,
轴有且只有一个公共点,
方程.files/image228.gif) 仅有一个实数根 14分
仅有一个实数根 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com