
题目列表(包括答案和解析)
(本题满分共12分)某流感病研究中心对温差与甲型H1N1病毒感染数之间的相关关系进行研究,他们每天将实验室放入数量相同的甲型H1N1病毒和100头猪,然后分别记录了4月1日至4月5日每天昼夜温差与实验室里100头猪的感染数,得到如下资料:
| 日 期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
| 温 差 | 10 | 13 | 11 | 12 | 7 |
| 感染数 | 23 | 32 | 24 | 29 | 17 |
(1)求这5天的平均感染数;(2)从4月1日至4月5日中任取2天,记感染数分别为![]() 用
用![]() 的形式列出所有的基本事件, 其中
的形式列出所有的基本事件, 其中![]() 视为同一事件,并求
视为同一事件,并求![]() 的事件A的概率。
的事件A的概率。
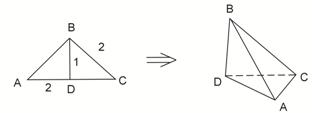 (本题满分共12分)如图,在
(本题满分共12分)如图,在![]() 中,
中,![]() 为
为![]() 边上高,
边上高,![]() ,
,![]() ,沿
,沿![]() 将
将![]() 翻折,使得
翻折,使得![]() ,得到几何体
,得到几何体![]() 。(1)求证:
。(1)求证:![]() ;
;
(2)求![]() 与平面
与平面![]() 成角的正切值。
成角的正切值。
(本题共2小题,满分12分。第1小题满分6分,第2小题满分6分)
已知复数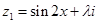 ,
,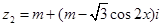 (
(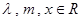 ),且
),且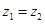 .
.
(1)设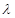 =
=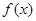 ,求
,求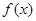 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
(2)当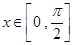 时,求函数
时,求函数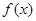 的值域.
的值域.
(本题满分12分)
设函数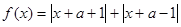 的图象关于y轴对称,函数
的图象关于y轴对称,函数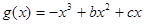 (b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线:
(b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线:
(1) 求f(x)的表达式;
(2) 试求b的值;
(3)
若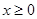 时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。
时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。
(本题满分13分)在4月份(按30天计算),有一新款服装投入某商场销售,4月1日该款服装仅销售出10件,第二天售出35件,第三天销售60件,然后,每天售出的件数分别递增25件,直到4月12日销售量达到最大,以后每天销售的件数分别递减15件.
(Ⅰ)问到月底该服装共销售出几件.
(Ⅱ)按规律,当该商场销售此服装的日销售量达到150件以上时,社会上就流行,问该款服装在社会上流行是否超过14天?并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com