
题目列表(包括答案和解析)
 ,
, )。
)。 |=|
|=| |,求角α的值;
|,求角α的值; ·
· ,求
,求 的值
的值
(本小题满分14分)
已知点C(1,0),点A、B是⊙O: 上任意两个不同的点,且满足
上任意两个不同的点,且满足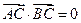 ,设P为弦AB的中点.
,设P为弦AB的中点.
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线 的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.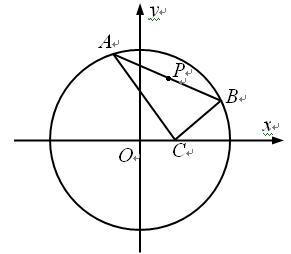
(本小题满分14分)已知点P(2,0),及圆C:x2+y2-6x+4y+4=0.
(1)当直线l过点P且与圆心C的距离为1时,求直线l的方程;
(2)设过点P的直线与圆C交于A、B两点,当|AB|=4,求以线段AB为直径的圆的方程.
(本小题满分14分)
已知点C(1,0),点A、B是⊙O: 上任意两个不同的点,且满足
上任意两个不同的点,且满足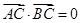 ,设P为弦AB的中点.
,设P为弦AB的中点.
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线 的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.

一、选择题:
1.D 2.D 3.B 4.A 5.C 6.A 7.B 8.A 9.C 10.A 11.C 12.D
二、填空题:13. -2 14.11 15. .files/image115.gif)
.files/image016.gif) ⊥
⊥.files/image020.gif) 或
或 .files/image117.gif)
.files/image016.gif) ⊥
⊥.files/image020.gif)
16.3 17..files/image119.gif) 18.
18..files/image121.gif)
三、解答题
19.解:(Ⅰ)记至少有一次中一等奖的事件为A,
则其概率P(A)=.files/image123.gif) +
+.files/image125.gif) =
=.files/image127.gif) .
.
答:至少有一次中一等奖的概率为.files/image127.gif) . ........................6分
. ........................6分
注:本小问缺少事件命名、答,各扣一分.
(Ⅱ)每次抽取奖券都是相互独立的,其中后四次分别看作独立重复实验. ........7分
设第一次中一等奖,后四次中恰有2次中二等奖的事件为B, ...........8分
则其概率P(B).files/image129.gif) =0.05292 .............................11分
=0.05292 .............................11分
答:第一次中一等奖,后四次中恰有2次中二等奖的概率为0.05292. ..........12分
20.解:(Ⅰ).files/image131.gif) .............................2分
.............................2分
由题意.files/image133.gif) ,代入上式,解之得:a=1,b=1. ..........5分
,代入上式,解之得:a=1,b=1. ..........5分
(2)当b=1时,.files/image135.gif)
.files/image137.gif)
因.files/image139.gif) 故方程有两个不同实根
故方程有两个不同实根.files/image141.gif) . ............8分
. ............8分
不妨设.files/image143.gif) ,由
,由.files/image145.gif) 可判断
可判断.files/image147.gif) 的符号如下:
的符号如下:
当.files/image149.gif)
.files/image147.gif) >0;
>0;
当.files/image152.gif)
.files/image147.gif) <0;
<0;
当.files/image154.gif)
.files/image147.gif) >0
>0
因此.files/image156.gif) 是极大值点,
是极大值点,.files/image158.gif) 是极小值点. ........................ 11分
是极小值点. ........................ 11分
所以,当b=1时,试证明:不论a取何实数,函数.files/image087.gif) 总有两个不同的极值点.....12分.
总有两个不同的极值点.....12分.
.files/image160.gif) 21.21.解:
21.21.解:
(Ⅰ)设P点在平面ABCD上的射影为O, 连接CO,则∠PCO就是PC与平面ABCD所成的角,--------------------------1分
取AB的中点M,连接PM、OM,因为PA=PB,所以PM⊥AB,由三垂线定理的逆定理得OM⊥AB,,所以∠PMO就是二面角P-AB-C的平面角,即∠PMO=600,--------------2分
在ΔPAB中,
PM=.files/image162.gif)
.files/image164.gif) 过O作ON⊥BC交BC于N,则BN=MO=1,
过O作ON⊥BC交BC于N,则BN=MO=1,
在RtΔCON中,OC=.files/image166.gif) ------------------------3分
------------------------3分
在RtΔPOC中 ,tan∠PCO=.files/image168.gif)
即PC与平面ABCD所成的角为arctan.files/image170.gif) .-------------------------------------5分
.-------------------------------------5分
(Ⅱ)连接AC、BD.交于点H,则H为AC的中点,取PC中点E,则PA∥HE,-----7分
.files/image172.gif) 所求。---9分
所求。---9分
(Ⅲ)取PA中点为F,连接HF,则HF∥PC,所以∠BHF为异面直线PC与BD所成的角或其补角。----------------10分
在ΔBHF中,.files/image174.gif)
.files/image176.gif) -------12分
-------12分
.files/image178.gif) COS∠BHF=
COS∠BHF=.files/image180.gif)
.files/image178.gif) ∠BHF=arccos
∠BHF=arccos.files/image182.gif) ,即PC与BD所成的角为 arccos
,即PC与BD所成的角为 arccos.files/image182.gif) 。--------14分
。--------14分
22.解:(Ⅰ)以AB中点为坐标原点,直线AB所在直线为x轴建立平面直角坐标系,则 A(-1,0),B(1,0)………………………………………1’
.files/image184.gif) 设M(x,y),由题意:|MP|=|MA|,|BP|=2,所以 |MB|+|MA|=2 ……..3’
设M(x,y),由题意:|MP|=|MA|,|BP|=2,所以 |MB|+|MA|=2 ……..3’
故曲线C是以A、B为焦点,长轴长为2的椭圆,……………………..5’
其方程为x2+2y2=2 ……………………….7’
(Ⅱ)直线l与曲线C的位置关系是相切。…………………8’
证明如下: 由(Ⅰ)知曲线C方程为x2+2y2=2,
设P(m,n),则P在⊙B上,故(m-1)2+n2=8,即m2+n2=7+2m …………..9’
当P、A、B共线时,直线l的方程为x=±,显然结论成立. ………….10’
当P、A、B 不共线时,直线l的方程为:y-=-(x-)
整理得,y=-(x-)+=-x+=-x+ ………………….11’
把直线l的方程代入曲线C方程得:x2+2(-x+)2=2
整理得,[n2+2(m+1)2]x2-4(m+1)(m+3)x+2(m+3)2-2n2=0 ………………………12’
.files/image186.gif) 判别式△=[4(m+1)(m+3)]2-4[n2+2(m+1)2]
[2(m+3)2-2n2]= -8n2[(m+3)2-n2-2(m+1)2]
判别式△=[4(m+1)(m+3)]2-4[n2+2(m+1)2]
[2(m+3)2-2n2]= -8n2[(m+3)2-n2-2(m+1)2]
=-8n2[-m2-n2+2m+7]=0
∴直线l与曲线C相切 ……………………………14’
说明:以A或B为原点建系,可参照得分.
另证:在直线l上任取一点M’,连结M’A、M’B、MA,……………………………9’
由垂直平分线的性质得 |M’A|=|M’P|,……………………………11’
∴|M’A|+|M’B|=|M’P|+|M’B|≥|PB|=2(当且仅当M、M’重合时取”=”号) ……13’
∴直线l与椭圆C有且仅有一个公共点M
结论得证. …………14’
23解:(Ⅰ);由Sn+2- (t+1)Sn+1+tSn=0,得(t+1)Sn+1= Sn+2+tSn,即.files/image188.gif) ,
(2分)
,
(2分)
而 a1=t,a2=t2 (3分)
所以,当t≠0时,数列.files/image102.gif) 是以t为首项,t为公比的等比数列.于是
是以t为首项,t为公比的等比数列.于是.files/image190.gif) 。
。
经验证当t=0时上述结论仍成立 (4分)
(Ⅱ)由(Ⅰ)可知.files/image192.gif) ,则有
,则有
.files/image194.gif)
.files/image196.gif) (5分)
(5分)
当t≠0时
.files/image198.gif) (6分)
(6分)
于是有.files/image200.gif) ,解得
,解得.files/image202.gif) (7分)
(7分)
所以.files/image204.gif)
经验证当t=0时上述结论仍成立 (9分)
(Ⅲ)=(tn+t-n) ∵(tn+t-n)-(2n+2-n)=(tn-2n)[1-()n] 且.files/image018.gif) <t<2
<t<2
∴<<1 ∴tn-2n<0且1-()n<0
∴(tn-2n) [1-()n]<0
∴tn+t-n<2n+2-n (11分)
∴ 2( ++ ……+)<(2+22+……+2n)+ (2-1+2-2+……+2-n)=2(2n-1)+1-2-n
=2n+1-(1+2-n) (12分)
<2n+1-2
∴.files/image111.gif) <
<.files/image113.gif) (14分)
(14分)
另解:对f(t)求导,可得函数.files/image206.gif) 在区间
在区间.files/image208.gif) 上单调减,在区间
上单调减,在区间.files/image210.gif) 上单调增,且f()=f(2)
上单调增,且f()=f(2)
于是有.files/image212.gif)
所以.files/image111.gif) <
<.files/image214.gif)
=.files/image216.gif)
.files/image218.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com