
题目列表(包括答案和解析)
(坐标系与参数方程选做题)已知圆的极坐标方程ρ=2cosθ,直线的极坐标方程为ρcosθ-2ρsinθ+7=0,则圆心到直线的距离为_______
(坐标系与参数方程选做题) 已知圆的极坐标方程![]() ,直线的极坐标方程为
,直线的极坐标方程为![]() ,则圆心到直线距离为 。
,则圆心到直线距离为 。
(坐标系与参数方程选做题)
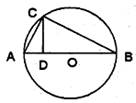
已知圆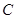 的参数方程为
的参数方程为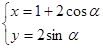 (
(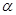 为参数).以原点为极点,
为参数).以原点为极点,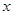 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线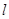 的极坐标方程为
的极坐标方程为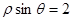 ,则直线
,则直线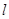 与圆
与圆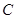 的交点的直角坐标为 .
的交点的直角坐标为 .
(坐标系与参数方程选做题)已知圆的极坐标方程ρ=2cosθ,直线的极坐标方程为
 ρcosθ-2ρsinθ+7=0,则圆心到直线的距离为_
ρcosθ-2ρsinθ+7=0,则圆心到直线的距离为_
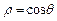 ,直线的极坐标方程为
,直线的极坐标方程为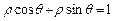 ,则圆心到直线距离为 。
,则圆心到直线距离为 。一、选择题(本大题共10小题,每小题5分,共50分)
1.D 2.B 3.C 4.C 5.D 6.B 7.C 8.A 9.C 10.B
二、填空题(本大题共4小题,每小题5分,共20分)
11.文科数学.files/image273.gif) 12.4 13.70,10,32 14.
12.4 13.70,10,32 14.文科数学.files/image275.gif) 15.
15.文科数学.files/image107.gif)
三、解答题(本大题共6小题,共80分)
16.(本小题满分12分)
解:(Ⅰ)文科数学.files/image278.gif) …………………………………2分
…………………………………2分
文科数学.files/image280.gif) ……………………………………………………3分
……………………………………………………3分
文科数学.files/image282.gif) ………………………………………………………5分
………………………………………………………5分
∴函数文科数学.files/image129.gif) 的最小正周期
的最小正周期文科数学.files/image285.gif) …………………………………………6分
…………………………………………6分
(Ⅱ)当文科数学.files/image196.gif) 时,
时,文科数学.files/image287.gif) ………………………………………8分
………………………………………8分
∴文科数学.files/image289.gif) ………………………………………………………………10分
………………………………………………………………10分
∴文科数学.files/image129.gif) 的值域是
的值域是文科数学.files/image291.gif) ………………………………………………………12分
………………………………………………………12分
17.(本小题满分12分)
解:设:用文科数学.files/image167.gif) 、
、文科数学.files/image169.gif) 、
、文科数学.files/image171.gif) 分别表示3枚钥匙,其中
分别表示3枚钥匙,其中文科数学.files/image167.gif) 是房门钥匙,则这个随机事件可看作是三枚钥匙的一个排序,它包含了:
是房门钥匙,则这个随机事件可看作是三枚钥匙的一个排序,它包含了:文科数学.files/image296.gif) 、
、文科数学.files/image298.gif) 、
、文科数学.files/image300.gif) 、
、文科数学.files/image302.gif) 、
、文科数学.files/image304.gif) 、
、文科数学.files/image306.gif) 共6个基本事件;………………………………4分
共6个基本事件;………………………………4分
(Ⅰ)设:用文科数学.files/image002.gif) 表示事件“恰好第三次打开房门锁”,则事件
表示事件“恰好第三次打开房门锁”,则事件文科数学.files/image002.gif) 包括
包括文科数学.files/image304.gif) 、
、文科数学.files/image306.gif) 共两个基本事件:……………………………………………………………………6分
共两个基本事件:……………………………………………………………………6分
文科数学.files/image311.gif) …………………………………………………………………………8分
…………………………………………………………………………8分
(Ⅱ)设:用文科数学.files/image004.gif) 表示事件“两次内打开房门锁”,则事件
表示事件“两次内打开房门锁”,则事件文科数学.files/image004.gif) 包含:
包含:文科数学.files/image296.gif) 、
、文科数学.files/image298.gif) 、
、文科数学.files/image300.gif) 、
、文科数学.files/image302.gif) 共4个基本事件:
共4个基本事件:文科数学.files/image318.gif) ………………………………………………………10分
………………………………………………………10分
答:恰好第三次打开房门锁的概率是文科数学.files/image320.gif) ,两次内打开的概率是
,两次内打开的概率是文科数学.files/image322.gif) . ……………12分
. ……………12分
18.(本小题满分14分)
(Ⅰ) 证明:依题意:文科数学.files/image324.gif) ,且
,且文科数学.files/image326.gif) 在平面
在平面文科数学.files/image209.gif) 外.……………………2分
外.……………………2分
∴文科数学.files/image207.gif) 平面
平面文科数学.files/image209.gif) …………………………………………………………………4分
…………………………………………………………………4分
(Ⅱ) 证明:连结文科数学.files/image330.gif)
∴文科数学.files/image338.gif) 平面
平面文科数学.files/image340.gif) …………5分
…………5分
又∵文科数学.files/image179.gif) 在
在文科数学.files/image343.gif) 上,∴
上,∴文科数学.files/image345.gif) 在平面
在平面文科数学.files/image340.gif) 上
上
∴文科数学.files/image347.gif) …………………………6分
…………………………6分
∵文科数学.files/image204.gif) ∴
∴文科数学.files/image350.gif)
∴文科数学.files/image352.gif)
∴文科数学.files/image354.gif) 中,
中,文科数学.files/image356.gif) ………………………………………7分
………………………………………7分
同理:文科数学.files/image358.gif)
∵文科数学.files/image360.gif) 中,
中,文科数学.files/image362.gif)
∴文科数学.files/image364.gif) ………………………………………………………………………8分
………………………………………………………………………8分
∴文科数学.files/image211.gif) 平面
平面文科数学.files/image209.gif) ……………………………………………………………10分
……………………………………………………………10分
(Ⅲ)解:∵文科数学.files/image211.gif) 平面
平面文科数学.files/image209.gif)
∴所求体积文科数学.files/image368.gif) ……………………………………………12分
……………………………………………12分
文科数学.files/image370.gif) …………………………………………14分
…………………………………………14分
19.(本小题满分14分)
解:(Ⅰ) 根据题意,得
文科数学.files/image372.gif) ………………………………………………………3分
………………………………………………………3分
解得文科数学.files/image374.gif) ……………………………………………………………………6分
……………………………………………………………………6分
(Ⅱ)由(Ⅰ) 文科数学.files/image376.gif)
文科数学.files/image127.jpg)
∴文科数学.files/image378.gif) ……………………10分
……………………10分
∴文科数学.files/image380.gif) ………………14分
………………14分
20.(本小题满分14分)
解:(Ⅰ) 依题意:文科数学.files/image382.gif) . ……………………………………………………2分
. ……………………………………………………2分
∴文科数学.files/image384.gif) ∴所求方程为
∴所求方程为文科数学.files/image386.gif) . ……………………………………………4分
. ……………………………………………4分
(Ⅱ)设动圆圆心为文科数学.files/image388.gif) ,(其中
,(其中文科数学.files/image390.gif) ),
),文科数学.files/image392.gif) 、
、文科数学.files/image394.gif) 的坐标分别为
的坐标分别为文科数学.files/image396.gif) ,
,文科数学.files/image398.gif)
因为圆文科数学.files/image245.gif) 过
过文科数学.files/image401.gif) ,故设圆的方程
,故设圆的方程文科数学.files/image403.gif) ……………6分
……………6分
∵文科数学.files/image392.gif) 、
、文科数学.files/image394.gif) 是圆
是圆文科数学.files/image245.gif) 和
和文科数学.files/image160.gif) 轴的交点
轴的交点文科数学.files/image127.jpg)
∴令文科数学.files/image406.gif) 得:
得:文科数学.files/image408.gif) …………………………………………………8分
…………………………………………………8分
则文科数学.files/image410.gif) ,
,文科数学.files/image412.gif)
文科数学.files/image414.gif) …………………10分
…………………10分
又∵圆心文科数学.files/image388.gif) 在抛物线
在抛物线文科数学.files/image237.gif) 上
上
∴文科数学.files/image418.gif) …………………………………………………………………11分
…………………………………………………………………11分
∴文科数学.files/image420.gif) ………………………………….12分
………………………………….12分
∴当文科数学.files/image422.gif) 时,
时,文科数学.files/image424.gif) (定值). ……………………………………………14分
(定值). ……………………………………………14分
21.(本小题满分14分)
解:由函数文科数学.files/image264.gif) 得,
得,文科数学.files/image426.gif) ………………3分
………………3分
(Ⅰ) 若文科数学.files/image129.gif) 为区间
为区间文科数学.files/image266.gif) 上的“凸函数”,则有
上的“凸函数”,则有文科数学.files/image430.gif) 在区间
在区间文科数学.files/image266.gif) 上恒成立,由二次函数的图像,当且仅当
上恒成立,由二次函数的图像,当且仅当
文科数学.files/image432.gif) ,
,文科数学.files/image127.jpg)
即文科数学.files/image434.gif)
文科数学.files/image436.gif) . …………………………………………………7分
. …………………………………………………7分
(Ⅱ)当文科数学.files/image269.gif) 时,
时,文科数学.files/image430.gif) 恒成立
恒成立文科数学.files/image440.gif) 当
当文科数学.files/image269.gif) 时,
时,文科数学.files/image442.gif) 恒成立.……………………………………………………………………………8分
恒成立.……………………………………………………………………………8分
当文科数学.files/image406.gif) 时,
时,文科数学.files/image445.gif) 显然成立。 …………………………………9分
显然成立。 …………………………………9分
当文科数学.files/image447.gif) ,
,文科数学.files/image449.gif)
∵文科数学.files/image081.gif) 的最小值是
的最小值是文科数学.files/image165.gif) .
.
∴文科数学.files/image453.gif) .
.
从而解得文科数学.files/image455.gif) …………………………………………………………………1分
…………………………………………………………………1分
当文科数学.files/image457.gif) ,
,文科数学.files/image459.gif)
∵文科数学.files/image081.gif) 的最大值是
的最大值是文科数学.files/image461.gif) ,∴
,∴文科数学.files/image463.gif) ,
,
从而解得文科数学.files/image465.gif) . ………………………………………………………………13分
. ………………………………………………………………13分
综上可得文科数学.files/image467.gif) ,从而
,从而文科数学.files/image469.gif) ………………………………14分
………………………………14分
如上各题若有其它解法,请评卷老师酌情给分.文科数学.files/image127.jpg)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com