
题目列表(包括答案和解析)
| 167 | 50 |
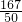 ,求a、b的值.
,求a、b的值.
 ,求a,b的值。
,求a,b的值。 
 ,求a、b的值.
,求a、b的值.一、选择题(本大题共8小题,每小题5分,共40分)
1.D 2.B 3.D 4.A 5.C 6.B 7.D 8.C
二、填空题(本大题共6小题,每小题5分,共30分)
9.理科数学.files/image317.gif) (
(理科数学.files/image319.gif) ) 10.12000
11.4 12.144 13.
) 10.12000
11.4 12.144 13.理科数学.files/image321.gif)
14.理科数学.files/image323.gif) 15.
15.理科数学.files/image325.gif)
三、解答题(本大题共6小题,共80分)
16.(本小题满分12分)
解:(Ⅰ)理科数学.files/image327.gif) …………………………………2分
…………………………………2分
理科数学.files/image329.gif) ……………………………………………………3分
……………………………………………………3分
理科数学.files/image331.gif) ………………………………………………………5分
………………………………………………………5分
∴函数理科数学.files/image138.gif) 的最小正周期
的最小正周期理科数学.files/image334.gif) …………………………………………6分
…………………………………………6分
(Ⅱ)当理科数学.files/image213.gif) 时,
时,理科数学.files/image336.gif) ………………………………………8分
………………………………………8分
∴当理科数学.files/image338.gif) 即
即理科数学.files/image340.gif) 时,函数
时,函数理科数学.files/image138.gif) 单调递增……………………10分
单调递增……………………10分
当理科数学.files/image343.gif) 即
即理科数学.files/image345.gif) 时,函数
时,函数理科数学.files/image138.gif) 单调递减……………………12分
单调递减……………………12分
17.(本小题满分12分)
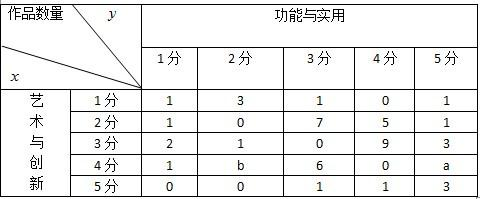
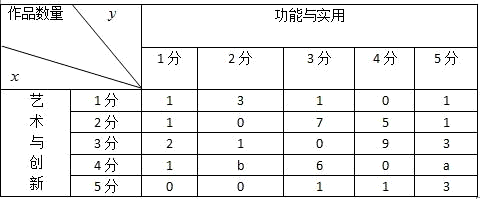
解:∵作品数量共有50件,∴理科数学.files/image347.gif) …………①……………………2分
…………①……………………2分
(Ⅰ)从表中可以看出,“艺术与创新为4分且功能与实用为3分”的作品数量为6件,
∴“艺术与创新为4分且功能与实用为3分”的概率为理科数学.files/image349.gif) ……………4分
……………4分
(Ⅱ)由表可知“功能与实用”得分理科数学.files/image170.gif) 有1分、2分、3分、4分、5分五个等级,且每个等级分别有5件,
有1分、2分、3分、4分、5分五个等级,且每个等级分别有5件,理科数学.files/image352.gif) 件,15件,15件,
件,15件,15件,理科数学.files/image354.gif) 年。
年。
∴“功能与实用”得分理科数学.files/image170.gif) 的分布列为:
的分布列为:
理科数学.files/image170.gif)
1
2
3
4
5
理科数学.files/image358.gif)
理科数学.files/image360.gif)
理科数学.files/image362.gif)
理科数学.files/image364.gif)
理科数学.files/image364.gif)
理科数学.files/image367.gif)
…………………………………8分
又∵“功能与实用”得分的数学期望为理科数学.files/image220.gif) ,
,
∴理科数学.files/image370.gif)
与①式联立可解得:理科数学.files/image372.gif) ,
,理科数学.files/image374.gif) ……………………12分
……………………12分
18.(本小题满分14分)
解:(Ⅰ)在理科数学.files/image376.gif) 中,
中,理科数学.files/image378.gif) ,
,理科数学.files/image380.gif) ,∴
,∴理科数学.files/image382.gif) ,
,理科数学.files/image384.gif) ……1分
……1分
在理科数学.files/image386.gif) 中,
中,理科数学.files/image384.gif) ,
,理科数学.files/image388.gif) ,∴
,∴理科数学.files/image390.gif) ,
,理科数学.files/image392.gif) …………2分
…………2分
∴理科数学.files/image394.gif) …………4分
…………4分
则理科数学.files/image396.gif) …………………………………………5分
…………………………………………5分
(Ⅱ)∵理科数学.files/image233.gif) 平面
平面理科数学.files/image126.gif) ,∴
,∴理科数学.files/image400.gif) …………………………6分
…………………………6分
理科数学.files/image402.jpg) 又
又理科数学.files/image404.gif) ,
,理科数学.files/image406.gif) ,
,
∴理科数学.files/image408.gif) 平面
平面理科数学.files/image410.gif) ………………………7分
………………………7分
∵理科数学.files/image236.gif) 、
、理科数学.files/image245.gif) 分别为
分别为理科数学.files/image238.gif) 、
、理科数学.files/image247.gif) 中点,
中点,
∴理科数学.files/image416.gif) ………………………8分
………………………8分
∴理科数学.files/image418.gif) 平面
平面理科数学.files/image410.gif) ………………………9分
………………………9分
∵理科数学.files/image420.gif) 平面
平面理科数学.files/image251.gif) ,∴平面
,∴平面理科数学.files/image249.gif) 平面
平面理科数学.files/image251.gif)
………………………10分
(Ⅲ)取理科数学.files/image108.gif) 的中点
的中点理科数学.files/image284.gif) ,连结
,连结理科数学.files/image426.gif) ,则
,则理科数学.files/image428.gif) ,
,
∴理科数学.files/image430.gif) 平面
平面理科数学.files/image432.gif) ,过
,过理科数学.files/image284.gif) 作
作理科数学.files/image434.gif) 于
于理科数学.files/image436.gif) ,
,
连接理科数学.files/image438.gif) ,则
,则理科数学.files/image440.gif) 为二面角
为二面角理科数学.files/image253.gif) 的平面角。
的平面角。
…………………………12分
∵理科数学.files/image284.gif) 为
为理科数学.files/image108.gif) 的中点,
的中点,理科数学.files/image434.gif) ,
,理科数学.files/image445.gif) ,
,
∴理科数学.files/image447.gif) ,又
,又理科数学.files/image449.gif) ,
,
∴理科数学.files/image451.gif) ,故
,故理科数学.files/image453.gif)
即三面角理科数学.files/image253.gif) 的大小为
的大小为理科数学.files/image455.gif) …………………………14分
…………………………14分
19.(本小题满分14分)
解:由函数理科数学.files/image266.gif) 得,
得,理科数学.files/image457.gif) ………………3分
………………3分
(Ⅰ) 若理科数学.files/image138.gif) 为区间
为区间理科数学.files/image268.gif) 上的“凸函数”,则有
上的“凸函数”,则有理科数学.files/image461.gif) 在区间
在区间理科数学.files/image268.gif) 上恒成立,由二次函数的图像,当且仅当
上恒成立,由二次函数的图像,当且仅当
理科数学.files/image463.gif) ,
,
即理科数学.files/image465.gif)
理科数学.files/image467.gif) . …………………………………………………7分
. …………………………………………………7分
(Ⅱ)当理科数学.files/image272.gif) 时,
时,理科数学.files/image461.gif) 恒成立
恒成立理科数学.files/image471.gif) 当
当理科数学.files/image272.gif) 时,
时,理科数学.files/image473.gif) 恒成立.……………………………………………………………………………8分
恒成立.……………………………………………………………………………8分
当理科数学.files/image475.gif) 时,
时,理科数学.files/image477.gif) 显然成立。 …………………………………9分
显然成立。 …………………………………9分
当理科数学.files/image479.gif) ,
,理科数学.files/image481.gif)
∵理科数学.files/image270.gif) 的最小值是
的最小值是理科数学.files/image176.gif) .
.
∴理科数学.files/image485.gif) .
.
从而解得理科数学.files/image118.gif) …………………………………………………………………11分
…………………………………………………………………11分
当理科数学.files/image488.gif) ,
,理科数学.files/image490.gif)
∵理科数学.files/image270.gif) 的最大值是
的最大值是理科数学.files/image492.gif) ,∴
,∴理科数学.files/image494.gif) ,
,
从而解得理科数学.files/image496.gif) . ………………………………………………………………13分
. ………………………………………………………………13分
综上可得理科数学.files/image498.gif) ,从而
,从而理科数学.files/image500.gif) ………………………………14分
………………………………14分
20.(本小题满分14分)
解:(Ⅰ)∵抛物线理科数学.files/image276.gif) 的焦点为
的焦点为理科数学.files/image503.gif) (
(理科数学.files/image280.gif) ),………………………1分
),………………………1分
∴理科数学.files/image506.gif) ………………………………………………………………………2分
………………………………………………………………………2分
∴理科数学.files/image508.gif) ,所求方程为
,所求方程为理科数学.files/image510.gif) ………………………………………4分
………………………………………4分
(Ⅱ)设动圆圆心为理科数学.files/image512.gif) ,(其中
,(其中理科数学.files/image514.gif) ),
),理科数学.files/image236.gif) 、
、理科数学.files/image245.gif) 的坐标分别为
的坐标分别为理科数学.files/image518.gif) ,
,理科数学.files/image520.gif)
因为圆理科数学.files/image284.gif) 过
过理科数学.files/image523.gif) ,故设圆的方程
,故设圆的方程理科数学.files/image525.gif) ……………6分
……………6分
∵理科数学.files/image236.gif) 、
、理科数学.files/image245.gif) 是圆
是圆理科数学.files/image284.gif) 和
和理科数学.files/image170.gif) 轴的交点
轴的交点
∴令理科数学.files/image475.gif) 得:
得:理科数学.files/image529.gif) …………………………………………………8分
…………………………………………………8分
则理科数学.files/image531.gif) ,
,理科数学.files/image533.gif)
理科数学.files/image535.gif) …………………10分
…………………10分
又∵圆心理科数学.files/image512.gif) 在抛物线
在抛物线理科数学.files/image276.gif) 上
上
∴理科数学.files/image539.gif) …………………………………………………………………11分
…………………………………………………………………11分
∴理科数学.files/image541.gif) ………………………………….12分
………………………………….12分
∴当理科数学.files/image508.gif) 时,
时,理科数学.files/image544.gif) (定值). ……………………………………………14分
(定值). ……………………………………………14分
21.(本小题满分14分)
解:(Ⅰ)若理科数学.files/image303.gif) 为等比数列,则存在
为等比数列,则存在理科数学.files/image546.gif) ,使
,使
理科数学.files/image548.gif) 对
对理科数学.files/image550.gif) 成立。…………………2分
成立。…………………2分
由已知:理科数学.files/image295.gif) ,代入上式,整理得
,代入上式,整理得
理科数学.files/image553.gif) ………①……………4分
………①……………4分
∵①式对理科数学.files/image550.gif) 成立,
成立,理科数学.files/image096.jpg)
∴理科数学.files/image555.gif) 解得
解得理科数学.files/image557.gif) ……………………………………5分
……………………………………5分
∴当理科数学.files/image559.gif) ,
,理科数学.files/image561.gif) 时,数列
时,数列理科数学.files/image303.gif) 是公比为2的等比数列…………6分
是公比为2的等比数列…………6分
(Ⅱ)证明:由(Ⅰ)得:理科数学.files/image563.gif) ,即
,即理科数学.files/image565.gif)
所以理科数学.files/image567.gif) ……………………………8分
……………………………8分
∵理科数学.files/image569.gif) …………………………9分
…………………………9分
理科数学.files/image313.gif) 时,
时,理科数学.files/image572.gif)
理科数学.files/image574.gif) …………………………11分
…………………………11分
现证:理科数学.files/image576.gif) (
(理科数学.files/image313.gif) )
)
证法1:
当理科数学.files/image579.gif) 时,
时,理科数学.files/image581.gif) ,
,理科数学.files/image096.jpg)
而理科数学.files/image583.gif) ,
,理科数学.files/image585.gif) ,故
,故理科数学.files/image579.gif) 时成立。…………………………12分
时成立。…………………………12分
理科数学.files/image587.gif) 时,由
时,由理科数学.files/image589.gif)
理科数学.files/image591.gif)
理科数学.files/image593.gif)
理科数学.files/image595.gif)
且理科数学.files/image597.gif) 得,
得,理科数学.files/image599.gif) ,∴
,∴理科数学.files/image601.gif) …………………14分
…………………14分
证法2:
理科数学.files/image313.gif) 时
时
理科数学.files/image604.gif)
理科数学.files/image605.gif)
理科数学.files/image607.gif)
理科数学.files/image311.gif) 个
个
理科数学.files/image610.gif)
∴理科数学.files/image576.gif) ……………………………………14分
……………………………………14分
证法3:理科数学.files/image096.jpg)
(1)理科数学.files/image579.gif) 时,
时,理科数学.files/image581.gif)
理科数学.files/image583.gif) ,故
,故理科数学.files/image579.gif) 时不等式成立……………………12分
时不等式成立……………………12分
(2)假设理科数学.files/image613.gif) (
(理科数学.files/image615.gif) )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com