
题目列表(包括答案和解析)
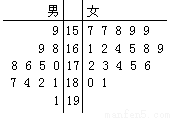
(本题满分12分)第26届世界大学生夏季运动会将于2011年11月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”和“非高个子”中中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用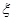 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出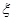 的分布列,并求
的分布列,并求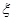 的数学期望。
的数学期望。
(本题满分18分,其中第1小题5分,第2小题5分,第3小题8分)
在平面直角坐标系中,已知 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为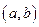 ,点
,点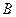 的坐标为
的坐标为 ,其中
,其中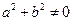 且
且 .设
.设 .
.
(1)若 ,
,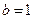 ,
,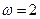 ,求方程
,求方程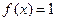 在区间
在区间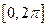 内的解集;
内的解集;
(2)若点 是过点
是过点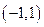 且法向量为
且法向量为 的直线
的直线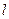 上的动点.当
上的动点.当 时,设函数
时,设函数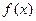 的值域为集合
的值域为集合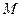 ,不等式
,不等式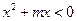 的解集为集合
的解集为集合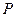 . 若
. 若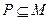 恒成立,求实数
恒成立,求实数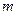 的最大值;
的最大值;
(3)根据本题条件我们可以知道,函数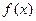 的性质取决于变量
的性质取决于变量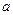 、
、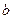 和
和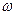 的值. 当
的值. 当 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数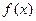 满足“图像关于点
满足“图像关于点 对称,且在
对称,且在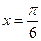 处
处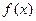 取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
.(本题满分18分)
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设二次函数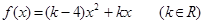 ,对任意实数
,对任意实数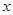 ,有
,有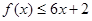 恒成立;数列
恒成立;数列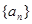 满足
满足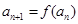 .
.
(1)求函数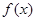 的解析式和值域;
的解析式和值域;
(2)试写出一个区间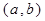 ,使得当
,使得当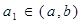 时,数列
时,数列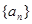 在这个区间上是递增数列,
在这个区间上是递增数列,
并说明理由;
(3)已知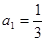 ,是否存在非零整数
,是否存在非零整数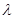 ,使得对任意
,使得对任意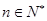 ,都有
,都有

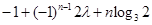 恒成立,若存在,
恒成立,若存在,
求之;若不存在,说明理由.
(本题满分12分)为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
|
分组 |
频数 |
频率 |
|
60.5~70.5 |
|
0.16 |
|
70.5~80.5 |
10 |
|
|
80.5~90.5 |
18 |
0.36 |
|
90.5~100.5 |
|
|
|
合计 |
50 |
|
(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号;
(2)填充频率分布表的空格(将答案直接填在表格内),并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
(本题满分18分;第(1)小题5分,第(2)小题5分,第(3)小题8分)
设数列![]() 是等差数列,且公差为
是等差数列,且公差为![]() ,若数列
,若数列![]() 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
(1)若![]() ,求证:该数列是“封闭数列”;
,求证:该数列是“封闭数列”;
(2)试判断数列![]() 是否是“封闭数列”,为什么?
是否是“封闭数列”,为什么?
(3)设![]() 是数列
是数列![]() 的前
的前![]() 项和,若公差
项和,若公差![]() ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使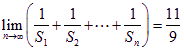 ;若存在,求
;若存在,求![]() 的通项公式,若不存在,说明理由.
的通项公式,若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com