
题目列表(包括答案和解析)
阅读某同学解分式方程的具体过程,回答后面问题.
解方程![]() .
.
【答案】解:原方程可化为:
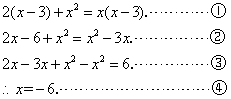
检验:当![]() 时,各分母均不为0,
时,各分母均不为0,
∴![]() 是原方程的解.
是原方程的解. ![]() ⑤
⑤
请回答:(1)第①步变形的依据是 ;
(2)从第 步开始出现了错误,这一步错误的原因是 __;
(3)原方程的解为 .
【答案】14![]() 。
。
【考点】轴对称-最短路线问题;勾股定理;垂径定理.
【专题】探究型.
【分析】先由MN=20求出⊙O的半径,再连接OA、OB,由勾股定理得出OD、OC的长,作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,在Rt△AB′E中利用勾股定理即可求出AB′的值.
【解答】∵MN=20,
∴⊙O的半径=10,
连接OA、OB,
在Rt△OBD中,OB=10,BD=6,
∴OD=![]() =
=![]() =8;
=8;
同理,在Rt△AOC中,OA=10,AC=8,
∴OC=![]() =
=![]() =6,
=6,
∴CD=8+6=14,
作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,
在Rt△AB′E中,
∵AE=AC+CE=8+6=14,B′E=CD=14,
∴AB′=![]() =
=![]() =14
=14![]() .
.
故答案为:14![]() .
.
【点评】本题考查的是轴对称-最短路线问题、垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
【解题思路】通过读题、审题
(1)完成表格有2个思路:从供或需的角度考虑,均能完成上表。
(2)运用公式(调运水的重量×调运的距离)
总调运量=A的总调运量+B的总调运量调运水的重量×调运的距离
y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275(注:一次函数的最值要得到自变量的取值范围)∵5>0∴y随x的增大而增大,y要最小则x应最大
由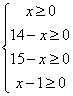 解得1≤x≤14
解得1≤x≤14
y=5x+1275中∵5>0∴y随x的增大而增大,y要最小则x应最小=1
∴调运方案为A往甲调1吨,往乙调13吨;B往甲调14吨,不往乙调。
【答案】⑴(从左至右,从上至下)14-x 15-x x-1
⑵y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275
解不等式1≤x≤14
所以x=1时y取得最小值
y=5+1275=1280
∴调运方案为A往甲调1吨,往乙调13吨;B往甲调14吨,不往乙调。

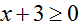 时,原方程可化为一元一次方程:
时,原方程可化为一元一次方程: ,所以
,所以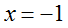 ;
;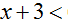 0,原方程可以化为一元一次方程:
0,原方程可以化为一元一次方程: =2,所以
=2,所以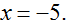
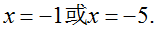
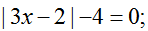
 的解也是方程
的解也是方程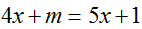 的解,求m的值.
的解,求m的值.【答案】![]() π.
π.
【考点】扇形面积的计算;三角形内角和定理.
【分析】根据三角形内角和定理得到∠B+∠C=180°-∠A=130°,利用半径相等得到OB=OD,OC=OE,则∠B=∠ODB,∠C=∠OEC,再根据三角形内角和定理得到∠BOD=180°-2∠B,∠COE=180°-2∠C,则∠BOD+∠COE=360°-2(∠B+∠C)=360°-2×130°=100°,图中阴影部分由两个扇形组成,它们的圆心角的和为100°,半径为3,然后根据扇形的面积公式计算即可.
【解答】∵∠A=50°,
∴∠B+∠C=180°-∠A=130°,
而OB=OD,OC=OE,
∴∠B=∠ODB,∠C=∠OEC,
∴∠BOD=180°-2∠B,∠COE=180°-2∠C,
∴∠BOD+∠COE=360°-2(∠B+∠C)
=360°-2×130°=100°,
而OB=![]() BC=3,
BC=3,
∴S阴影部分=![]() =
=![]() π.
π.
故答案为![]() π.
π.
【点评】本题考查了扇形面积的计算:扇形的面积=![]() (n为圆心角的度数,R为半径).也考查了三角形内角和定理.
(n为圆心角的度数,R为半径).也考查了三角形内角和定理.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com