
题目列表(包括答案和解析)
已知焦点在 轴上的椭圆
轴上的椭圆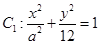 和双曲线
和双曲线 的离心率互为倒数,它们在第一象限交点的坐标为
的离心率互为倒数,它们在第一象限交点的坐标为 ,设直线
,设直线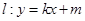 (其中
(其中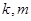 为整数).
为整数).
(1)试求椭圆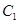 和双曲线
和双曲线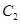 的标准方程;
的标准方程;
(2)若直线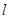 与椭圆
与椭圆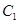 交于不同两点
交于不同两点 ,与双曲线
,与双曲线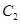 交于不同两点
交于不同两点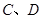 ,问是否存在直线
,问是否存在直线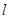 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
已知焦点在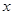 轴上的椭圆
轴上的椭圆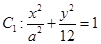 和双曲线
和双曲线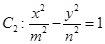 的离心率互为倒数,它们在第一象限交点的坐标为
的离心率互为倒数,它们在第一象限交点的坐标为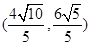 ,设直线
,设直线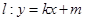 (其中
(其中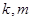 为整数).
为整数).
(1)试求椭圆 和双曲线
和双曲线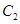 的标准方程;
的标准方程;
(2)若直线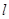 与椭圆
与椭圆 交于不同两点
交于不同两点 ,与双曲线
,与双曲线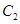 交于不同两点
交于不同两点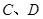 ,问是否存在直线
,问是否存在直线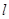 ,使得向量
,使得向量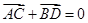 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
 轴上的椭圆
轴上的椭圆 和双曲线
和双曲线 的离心率互为倒数,它们在第一象限交点的坐标为
的离心率互为倒数,它们在第一象限交点的坐标为 ,设直线
,设直线 (其中
(其中 为整数).
为整数). 和双曲线
和双曲线 的标准方程;
的标准方程; 与椭圆
与椭圆 交于不同两点
交于不同两点 ,与双曲线
,与双曲线 交于不同两点
交于不同两点 ,问是否存在直线
,问是否存在直线 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. 的离心率为e,且b,e,
的离心率为e,且b,e, 为等比数列,曲线y=8-x2恰好过椭圆的焦点.
为等比数列,曲线y=8-x2恰好过椭圆的焦点. 的顶点和焦点分别是椭圆C1的焦点和顶点,设O为坐标原点,点A,B分别是C1和C2上的点,问是否存在A,B满足
的顶点和焦点分别是椭圆C1的焦点和顶点,设O为坐标原点,点A,B分别是C1和C2上的点,问是否存在A,B满足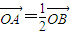 .请说明理由.若存在,请求出直线AB的方程.
.请说明理由.若存在,请求出直线AB的方程.| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
| x2 |
| m2 |
| y2 |
| n2 |
| OA |
| 1 |
| 2 |
| OB |
一.1.B 2.B 3.A 4.B 5.A 6.D 7.C 8.A 9.A 10.C
二.11.5
12.36
13. 14.
14. 
15. 适合① ②
②
 的不等式如:
的不等式如: ,
,  或其它曲线型只要适合即可
或其它曲线型只要适合即可
三.16.解: (1)



∴ 即AB边的长度为2.
…………… …………5分
即AB边的长度为2.
…………… …………5分
(2)由已知及(1)有:

∴ ……………8分
……………8分
由正弦定理得:  ……………10分
……………10分
∴ =
= …………12分
…………12分
17.解: ①依题意可设 ………1分
………1分
则
对n=1,2,3,……都成立 ………3分

∴ 又 解得
解得

∴ ………6分
………6分
②∵
 …………9分
…………9分
∴ +
+  +
+ +…+
+…+
 ……12分
……12分
18.解:(Ⅰ)依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事件B,
则 …………3分
…………3分
∵“甲、乙两人各投球一次,都没有命中”的事件为
 …………5分
…………5分
(Ⅱ)∵甲、乙两人在罚球线各投球二次时,
甲命中1次,乙命中0次的概率为 …………7分
…………7分
甲命中2次,乙命中0次的概率为 …………9分
…………9分
甲命中2次,乙命中1次”的概率为 …………11分
…………11分
故甲、乙两人在罚球线各投球两次,甲投球命中的次数比乙投球命中的次数多的
概率为P= …………12分
…………12分
 19.解法1:取BE的中点O,连OC.
19.解法1:取BE的中点O,连OC.
∵BC=CE, ∴OC⊥BE.又AB⊥平面BCE.
以O为原点建立空间直角坐标系O-xyz如图,
则由已知条件有: ,
, ,
,

 ,
, ……4分
……4分
设平面ADE的法向量为n= ,
,
则由n?



及n?



可取n
 ……6分
……6分
又AB⊥平面BCE. ∴AB⊥OC.OC⊥平面ABE
∴平面ABE的法向量可取为m= .
.
∵n?m
 ?
? =0,
=0,
∴n⊥m∴平面ADE⊥平面ABE. ……8分
⑵点C到平面ADE的距离为 ……12分
……12分
解法2:取BE的中点O,AE的中点F,连OC,OF,CD.则


 ∵AB⊥平面BCE,CD⊥平面BCE, AB=2CD
∵AB⊥平面BCE,CD⊥平面BCE, AB=2CD
∴CD 
 ,
,
 CD∴
CD∴ ∥ FD ……3分
∥ FD ……3分
∵BC=CE, ∴OC⊥BE.又AB⊥平面BCE.
∴OC⊥平面ABE. ∴FD⊥平面ABE.
从而平面ADE.⊥平面ABE. ……6分
②∵CD 
 ,延长AD, BC交于T
,延长AD, BC交于T
则C为BT的中点.
点C到平面ADE的距离等于点B到平面ADE的距离的 .……8分
.……8分
过B作BH⊥AE,垂足为H。∵平面ADE.⊥平面ABE。∴BH⊥平面BDE.
由已知有AB⊥BE.
BE= ,AB= 2, ∴BH=
,AB= 2, ∴BH= ,
,
从而点C到平面ADE的距离为 ……………… ……………12分
……………… ……………12分
或 ∥ FD, 点C到平面ADE的距离等于点O到平面ADE的距离为
∥ FD, 点C到平面ADE的距离等于点O到平面ADE的距离为 .
.
或取A B的中点M。易证 ∥ DA。点C到平面ADE的距离等于点M到平面ADE的距离为
∥ DA。点C到平面ADE的距离等于点M到平面ADE的距离为 .
.
20. 解:
(I)设O为原点,则
 =2
=2 ,
,
 =2
=2 。
。
而
 =
= ,得
,得 =
=
 ,
,
于是O、P、Q三点共线。 ……………2分
因为 所以PF∥QF/,且
所以PF∥QF/,且  ,……………3分
,……………3分
得



 ,
,
∴ ∴
∴ ……………5分
……………5分
因此椭圆的离心率为 双曲线的离心率为
双曲线的离心率为 ……………7分
……………7分
(II)设 、
、 ,
,
点P在双曲线 的上,有
的上,有 。
。
则 .
.
所以 。 ①…………9分
。 ①…………9分
又由点Q在椭圆 上,有
上,有 。
。
同理可得 ②
……………10分
②
……………10分
∵O、P、Q三点共线。∴ 。
。
由①、②得 。
……………13分
。
……………13分
21. 解:(I)
 ……………1分
……………1分
由已知有: ∴
∴ ,∴
,∴ ……………3分
……………3分
从而

令 =0得:x1=1,x2=
=0得:x1=1,x2= . ∵
. ∵ ∴x2
∴x2
当x变化时, 、f(x)的变化情况如下表:
、f(x)的变化情况如下表:
x




+
-
+

增函数
减函数
增函数
从上表可知: 在
在 ,
, 上是增函数;
上是增函数;
在 ,上是减函数 ……………6分
,上是减函数 ……………6分
(II)∵m>0,∴m+1>1. 由(I)知:
①当0<m<1时, . 则最小值为
. 则最小值为 得:
得: ……8分
……8分
此时 .从而
.从而
∴最大值为 得
得
此时 适合. ……10分
适合. ……10分
②当m 1时,
1时,  在闭区间
在闭区间 上是增函数.
上是增函数.
∴最小值为
 ⑴
⑴
最大值为
 =0. ⑵………12分
=0. ⑵………12分
由⑵得: ⑶
⑶
⑶代入⑴得: .即
.即
又m 1,
1,  ∴
∴ 从而
从而
∴此时的a,m不存在
综上知:
 ,
, .
………14分
.
………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com