练习册

  • 练习册
  • 试题
    (一)主要知识: 1.数的概念的发展.复数的有关概念(实数.虚数.纯虚数.复数相等.共轭复数.模), 2.复数的代数表示与向量表示, 3.复数的加法与减法.复数的乘法与除法.复数的三角形式.复数三角形式的乘法与乘方.复数三角形式的除法与开方, 4.复数集中解实系数方程(包括一元二次方程.二项方程). 复数在过去几年里是代数的重要内容之一.涉及的知识面广.对能力要求较高.是高考热点之一.但随着新教材对复数知识的淡化.高考试题比例下降.因此考生要把握好复习的尺度. 从近几年的高考试题上看:复数部分考查的重点是基础知识题型和运算能力题型.基础知识部分重点是复数的有关概念.复数的代数形式.三角形式.两复数相等的充要条件及其应用.复平面内复数的几何表示及复向量的运算.主要考点为复数的模与辐角主值.共轭复数的概念和应用.若只涉及到一.二个知识点的试题大都集中在选择题和填空题,若涉及几个知识点的试题.往往是中.高档题目.解答此类问题一般要抓住相应的概念进行正确的变换.对有些题目.往往用数形结合可获得简捷的解法.有关复数n次乘方.求辐角等问题.涉及到复数的三角形式.首先要将所给复数转化为三角形式后再进行变换. 复数的运算是高考中复数部分的热点问题.主要考查复数的代数和三角形式的运算.复数模及辐角主值的求解及复向量运算等问题. 基于上述情况.我们在学习“复数 一章内容时.要注意以下几点: (1)复数的概念几乎都是解题的手段.因此在学习复数时要在深入理解.熟练掌握复数概念上下功夫.除去复数相等.模.辐角.共轭等外.还要注意一些重要而常不引起重视的概念.如:若有“3„„4 .就是说.而且很快联系到或.又∵是不可能的.∴. 复数的三角形式和代数式.提供了将“复数问题实数化 的手段. 复数的几何意义也是解题的一个重要手段. (2)对于涉及知识点多.与方程.三角.解析几何等知识综合运用的思想方法较多的题型.以及复数本身的综合题.一直成为学生的难点.应掌握规律及典型题型的技巧解法.并加以强化训练以突破此难点, (3)重视以下知识盲点: ①不能正确理解复数的几何意义.常常搞错向量旋转的方向, ②忽视方程的虚根成对出现的条件是实系数, ③盲目地将实数范围内数与形的一些结论.不加怀疑地引用到复数范围中来, ④容易混淆复数的有关概念.如纯虚数与虚数的区别问题.实轴与虚轴的交集问题.复数辐角主值的范围问题等. 【查看更多】

     

    题目列表(包括答案和解析)

    （2012•江苏一模）本题主要考查抛物线的标准方程、简单的几何性质等基础知识，考查运算求解、推理论证的能力．
    如图，在平面直角坐标系xOy，抛物线的顶点在原点，焦点为F（1，0）．过抛物线在x轴上方的不同两点A、B，作抛物线的切线AC、BD，与x轴分别交于C、D两点，且AC与BD交于点M，直线AD与直线BC交于点N．
    （1）求抛物线的标准方程；
    （2）求证：MN⊥x轴；
    （3）若直线MN与x轴的交点恰为F（1，0），求证：直线AB过定点．

    查看答案和解析>>

    从参加环保知识竞赛的学生中抽出60名，将其成绩(均为整数)整理后画出的频率分布直方图如图所示，观察图形，回答下列问题：

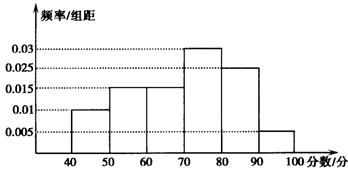
    ⑴80～90这一组的频数、频率分别是多少？

    ⑵估计这次环保知识竞赛的及格率(60分及以上为及格)． （本小题满分10分）

    【解析】本试题主要考查了统计和概率的综合运用。

    第一问频率：0.025×10＝0.25；……………3分

    频数：60×0.25＝15． ………………6分

    第二问0.015×10＋0.025×10＋0.03×10＋0.005×10＝0.75

    解：(1)频率：0.025×10＝0.25；……………3分

    频数：60×0.25＝15． ………………6分

    (2)0.015×10＋0.025×10＋0.03×10＋0.005×10＝0.75

     

    查看答案和解析>>


    同步练习册答案