
题目列表(包括答案和解析)
 (2005年上海高考题)用n个不同的实数a1,a2,…,an可得n!个不同的排列,每个排列为一行写成一个n!行的数阵.对第i行ai1,ai2,…,ain,记bi=-ai1+2ai2-3ai3+…+(-1)nnain,i=1,2,3,…,n!.用1,2,3可得数阵如右,由于此数阵中每一列各数之和都是12,所以,b1+b2+┄+b6=-12+2
(2005年上海高考题)用n个不同的实数a1,a2,…,an可得n!个不同的排列,每个排列为一行写成一个n!行的数阵.对第i行ai1,ai2,…,ain,记bi=-ai1+2ai2-3ai3+…+(-1)nnain,i=1,2,3,…,n!.用1,2,3可得数阵如右,由于此数阵中每一列各数之和都是12,所以,b1+b2+┄+b6=-12+2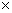 12-3
12-3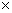 12=-24.那么,在用1,2,3,4,5形成的数阵中,b1+b2+┄+b120等于
12=-24.那么,在用1,2,3,4,5形成的数阵中,b1+b2+┄+b120等于
A.-3600 B.1800 C.-1080 D.-720
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com