
题目列表(包括答案和解析)
为了了解已有沙漠面积1000万公顷的某地区沙漠面积的变化情况,环保监测部门进入了连续4年的观察,并将每年年底的观察结果记录如表甲.根据这些数据还可绘制曲线图乙.由此预测到该地区沙漠的面积将继续扩大.
表甲

图乙

(1)如果不采取任何措施,那么到第m年底,该地区沙漠面积变为多少公倾?
(2)如果第5年底后,采取引水和植树造林等措施,使沙漠化扩大趋势得以减缓.第6年开始的每一年年底观察得该地区沙漠面积比上一年增加数y(公顷)分别为:a6,a7,a8,…,an,而a6,a7,a8,…,an还构成首项a6=32,公差d=-8的递减等差数列.当沙漠化扩大趋势停止后(即an=0),每年改造18万公顷沙漠,那么第n年底,该地区沙漠的面积能减少到980万公顷?
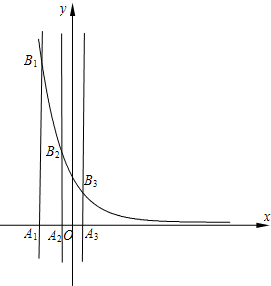 (2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(
(2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(| 1 | 2 |
 (2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(
(2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(| 1 | 2 |
如果以数列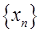 的任意连续三项作边长,都能构成一个三角形,那么称这样的数列
的任意连续三项作边长,都能构成一个三角形,那么称这样的数列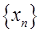 为“三角形”数列;又对于“三角形”数列
为“三角形”数列;又对于“三角形”数列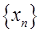 ,如果函数y=f(x)使得由
,如果函数y=f(x)使得由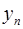 =f(
=f( )(
)( )确定的数列
)确定的数列 仍成为一个“三角形”数列,就称y=f(x) 是数列
仍成为一个“三角形”数列,就称y=f(x) 是数列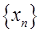 的“保三角形”函数。
的“保三角形”函数。
(Ⅰ)、已知数列 是首项为2012,公比为
是首项为2012,公比为 的等比数列,求证:
的等比数列,求证: 是“三角形”数列;
是“三角形”数列;
(Ⅱ)、已知数列 是首项为2,公差为1的等差数列,若函数f(x)=
是首项为2,公差为1的等差数列,若函数f(x)=  (m>0且m≠1)是
(m>0且m≠1)是 的“保三角形”函数. 求m的取值范围.
的“保三角形”函数. 求m的取值范围.
 的任意连续三项作边长,都能构成一个三角形,那么称这样的数列
的任意连续三项作边长,都能构成一个三角形,那么称这样的数列 为“三角形”数列;又对于“三角形”数列
为“三角形”数列;又对于“三角形”数列 ,如果函数y=f(x)使得由
,如果函数y=f(x)使得由 =f(
=f( )(
)( )确定的数列
)确定的数列 仍成为一个“三角形”数列,就称y="f(x)" 是数列
仍成为一个“三角形”数列,就称y="f(x)" 是数列 的“保三角形”函数。
的“保三角形”函数。 是首项为2012,公比为
是首项为2012,公比为 的等比数列,求证:
的等比数列,求证: 是“三角形”数列;
是“三角形”数列; 是首项为2,公差为1的等差数列,若函数f(x)=
是首项为2,公差为1的等差数列,若函数f(x)= (m>0且m≠1)是
(m>0且m≠1)是 的“保三角形”函数. 求m的取值范围.
的“保三角形”函数. 求m的取值范围.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com