
题目列表(包括答案和解析)
已知直线 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是 以极点为原点,极轴为x轴正方向建立直角坐标系,点
以极点为原点,极轴为x轴正方向建立直角坐标系,点 ,直线
,直线 与曲
与曲
线C交于A,B两点.
(1)写出直线 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(2)线段MA,MB长度分别记|MA|,|MB|,求|MA|·|MB|的值.
已知直线 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是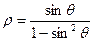 以极点为原点,极轴为x轴正方向建立直角坐标系,点
以极点为原点,极轴为x轴正方向建立直角坐标系,点 ,直线
,直线 与曲
与曲
线C交于A,B两点.
(1)写出直线 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(2)线段MA,MB长度分别记|MA|,|MB|,求|MA|·|MB|的值.
已知直线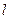 的参数方程为
的参数方程为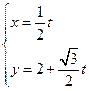 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是 以极点为原点,极轴为x轴正方向建立直角坐标系,点
以极点为原点,极轴为x轴正方向建立直角坐标系,点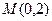 ,直线
,直线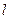 与曲线C交于A,B两点.
与曲线C交于A,B两点.
(1)写出直线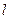 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(2)线段MA,MB长度分别记|MA|,|MB|,求|MA|·|MB|的值.
已知直线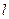 的参数方程为
的参数方程为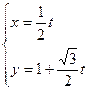 (
(
 为参数),曲线
为参数),曲线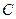 的极坐标方程为
的极坐标方程为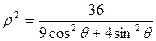
(1) 写出直线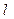 的极坐标方程与曲线
的极坐标方程与曲线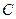 的普通方程;
的普通方程;
2)以极点为原点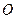 ,极轴为
,极轴为 轴正方向建立
轴正方向建立 直角坐标系,设直线
直角坐标系,设直线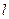 与曲线
与曲线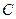 交于
交于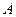 ,
,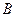 两点,求
两点,求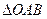 的面积.
的面积.
已知直线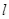 的参数方程为
的参数方程为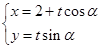 ,(
,(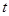 为参数,
为参数, 为倾斜角,且
为倾斜角,且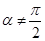 )与曲线
)与曲线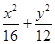 =1交于
=1交于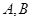 两点.
两点.
(I)写出直线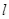 的一般方程及直线
的一般方程及直线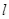 通过的定点
通过的定点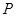 的坐标;
的坐标;
(Ⅱ)求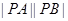 的最大值。
的最大值。
第Ⅰ部分 必考内容
一、填空题:
1. /江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image213.gif) 2.
2./江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image215.gif) 3.
3./江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image217.gif) 4.
4. /江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image219.gif)
5.
192 6./江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image221.gif) 7.
7. /江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image223.gif) 8.
8. /江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image225.gif)
9. 10. 640+80π cm3 11. 128 12. /江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image227.gif)
13. /江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image229.gif) 14.
14. /江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image231.gif)
二、解答题:
15.(本小题满分14分)
解 (1)/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image233.gif) ,
,
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image235.gif) .
.
(2) ω最大值为/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image237.gif) .
.
16.(本小题满分14分)
解 (1)/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image239.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image241.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image243.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image245.gif)
验证n=1时也满足上式:/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image247.gif)
(2)/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image249.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image251.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image253.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image255.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image257.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image259.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image261.jpg) 17.(本小题满分15分)
17.(本小题满分15分)
解 圆/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image085.gif) 化成标准方程为
化成标准方程为 /江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image264.gif) ,
,
先向左平移1个单位,然后向上平移2个单位后得⊙O方程为
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image266.gif)
由题意可得,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image268.gif) ,
,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image270.gif)
∴ /江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image272.gif) ,直线l:
,直线l:/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image274.gif)
由 /江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image276.gif) ,化简整理得
,化简整理得/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image278.gif) (*)
(*)
设/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image280.gif) ,则
,则/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image282.gif) 是方程(*)的两个实数根
是方程(*)的两个实数根
∴ /江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image284.gif) ,
,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image286.gif)
因为点C在圆上,所以/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image288.gif)
此时,(*)式中的/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image290.gif)
所求的直线l的方程为/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image292.gif) ,对应的C点的坐标为(-1,2);
,对应的C点的坐标为(-1,2);
或直线l的方程为/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image294.gif) ,对应的C点的坐标为(1,-2)
,对应的C点的坐标为(1,-2)
18.(本小题满分15分)
解 如图,连结/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image296.gif) ,由题意知,
,由题意知,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image298.gif) ,
,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image300.gif) ,
,
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image302.jpg)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image304.gif)
∴ 在/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image306.gif) 中,由余弦定理,可得
中,由余弦定理,可得
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image308.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image310.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image312.gif)
∴/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image314.gif) ,而
,而/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image298.gif) ,∴
,∴/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image306.gif) 是等腰三角形,
是等腰三角形,
∴/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image318.gif) ,
,
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image320.gif)
又 /江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image322.gif) ∴
∴ /江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image324.gif) 是等边三角形,
是等边三角形,
∴/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image326.gif) .
.
因此,乙船的速度的大小为/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image328.gif) (海里/小时).
(海里/小时).
答:乙船每小时航行/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image330.gif) 海里.
海里.
19.(本小题满分16分)
解 (1)由折起的过程可知,
PE⊥平面ABC,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image332.gif) ,
,
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image334.gif) ,
,
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image336.gif) ,
,
V(x)=/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image338.gif) (
(/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image340.gif) ).
).
(2)/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image342.gif) ,所以
,所以/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image344.gif) 时,
时,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image346.gif) ,V(x)单调递增;
,V(x)单调递增;/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image348.gif) 时,
时,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image350.gif) ,V(x)单调递减.因此x=6时,V(x)取得最大值
,V(x)单调递减.因此x=6时,V(x)取得最大值/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image352.gif) .
.
(3)/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image354.gif) ,
,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image356.gif) ,
,
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image358.gif) ,
,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image360.gif) ∥
∥/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image362.gif)
又/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image152.gif) 在平面
在平面/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image154.gif) 外,
外,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image365.gif) 平面
平面/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image154.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image367.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image152.gif) ∥平面
∥平面/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image154.gif) 。
。
20.(本小题满分16分)
解 (1)设/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image369.gif) 为椭圆
为椭圆/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image161.gif) 的左特征点,椭圆的左焦点为
的左特征点,椭圆的左焦点为/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image372.gif) ,可设直线
,可设直线/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image362.gif) 的方程为
的方程为/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image375.gif) .并将它代入
.并将它代入/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image161.gif) 得:
得:/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image378.gif) ,即
,即/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image380.gif) .设
.设/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image382.gif) ,则
,则/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image384.gif) ,
,
∵/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image386.gif) 被
被/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image145.gif) 轴平分,∴
轴平分,∴/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image389.gif) .即
.即/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image391.gif) .
.
即/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image393.gif) ,∴
,∴/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image395.gif) .
.
于是/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image397.gif) .∵
.∵/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image399.gif) ,即
,即/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image401.gif) .
.
(2)对于椭圆/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image403.gif) .于是猜想:椭圆
.于是猜想:椭圆/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image405.gif) 的“左特征点”是椭圆的左准线与
的“左特征点”是椭圆的左准线与/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image145.gif) 轴的交点.
轴的交点.
证明:设椭圆的左准线/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image189.gif) 与
与/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image145.gif) 轴相交于M点,过A,B分别作
轴相交于M点,过A,B分别作/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image189.gif) 的垂线,垂足分别为C,D.
的垂线,垂足分别为C,D.
据椭圆第二定义:/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image411.gif) ∵
∵/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image413.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image415.gif)
于是/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image417.gif) 即
即/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image419.gif) .∴
.∴/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image421.gif) ,又
,又/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image423.gif) 均为锐角,∴
均为锐角,∴/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image425.gif) ,∴
,∴/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image427.gif) .
.
∴/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image429.gif) 的平分线.故M为椭圆的“左特征点”.
的平分线.故M为椭圆的“左特征点”.
第Ⅱ部分 加试内容
一、解答题:
1. 解 函数/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image163.gif) 的零点:
的零点:/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image431.gif) ,
,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image433.gif) ,
,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image435.gif) .
.
又易判断出在/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image437.gif) 内,图形在
内,图形在/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image165.gif) 轴下方,在
轴下方,在/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image440.gif) 内,图形在
内,图形在/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image165.gif) 轴上方,
轴上方,
所以所求面积为/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image442.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image444.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image446.gif)
2. 解 (1)由/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image053.gif) 表示事件“购买该商品的3位顾客中至少有1位采用1期付款”.
表示事件“购买该商品的3位顾客中至少有1位采用1期付款”.
知/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image449.gif) 表示事件“购买该商品的3位顾客中无人采用1期付款”
表示事件“购买该商品的3位顾客中无人采用1期付款”
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image451.gif) ,
,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image453.gif) .
.
(2)/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image172.gif) 的可能取值为
的可能取值为/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image456.gif) 元,
元,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image458.gif) 元,
元,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image460.gif) 元.
元.
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image462.gif) ,
,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image464.gif) ,
,
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image466.gif) .
.
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image172.gif) 的分布列为
的分布列为
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image172.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image456.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image458.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image460.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image170.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image474.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image474.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image477.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image479.gif)
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image481.gif) (元).
(元).
二、解答题:
3. 解 (1)∵DE2=EF?EC,
∴DE : CE=EF: ED.
∵ÐDEF是公共角,
∴ΔDEF∽ΔCED. ∴ÐEDF=ÐC.
∵CD∥AP, ∴ÐC=Ð P.
∴ÐP=ÐEDF.
(2)∵ÐP=ÐEDF, ÐDEF=ÐPEA,
∴ΔDEF∽ΔPEA. ∴DE : PE=EF : EA.即EF?EP=DE?EA.
∵弦AD、BC相交于点E,∴DE?EA=CE?EB.∴CE?EB=EF?EP.
(3)∵DE2=EF?EC,DE=6,EF= 4, ∴EC=9.
∵CE : BE=3 : 2, ∴BE=6.
∵CE?EB=EF?EP,∴9×6=4×EP.解得:EP=/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image483.gif) .
.
∴PB=PE-BE=/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image485.gif) , PC=PE+EC=
, PC=PE+EC=/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image487.gif) .
.
由切割线定理得:PA2=PB?PC, ∴PA2=/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image485.gif) ×
×/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image487.gif) .∴PA=
.∴PA=/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image489.gif) .
.
4. 解 由题设条件,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image491.gif) ,
,
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image493.gif) ,即有
,即有/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image495.gif) ,
,
解得/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image497.gif) ,代入曲线
,代入曲线/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image180.gif) 的方程为
的方程为/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image499.gif) 。
。
所以将曲线/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image180.gif) 绕坐标原点逆时针旋转
绕坐标原点逆时针旋转/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image185.gif) 后,得到的曲线是
后,得到的曲线是/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image501.gif) 。
。
5. 解 (1)直线的参数方程为/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image503.gif) ,即
,即/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image505.gif) .
.
(2)把直线/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image505.gif) 代入
代入/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image195.gif) ,
,
得/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image507.gif) ,
,/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image509.gif) ,
,
则点/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image170.gif) 到
到/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image197.gif) 两点的距离之积为
两点的距离之积为/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image051.gif) .
.
6. 证明: ∵a、b、c均为实数,
∴/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image512.gif) (
(/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image201.gif) +
+/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image203.gif) )≥
)≥/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image516.gif) ≥
≥/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image211.gif) ,当a=b时等号成立;
,当a=b时等号成立;
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image512.gif) (
(/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image203.gif) +
+/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image205.gif) )≥
)≥/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image522.gif) ≥
≥/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image207.gif) ,当b=c时等号成立;
,当b=c时等号成立;
/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image512.gif) (
(/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image205.gif) +
+/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image201.gif) )≥
)≥/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image528.gif) ≥
≥/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image209.gif) .
.
三个不等式相加即得/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image201.gif) +
+/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image203.gif) +
+/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image205.gif) ≥
≥/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image207.gif) +
+/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image209.gif) +
+/江苏省沛县2009年高考数学全真模拟试卷(2009、1).files/image211.gif) ,当且仅当a=b=c时等号成立.
,当且仅当a=b=c时等号成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com