
题目列表(包括答案和解析)
对于任意的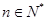 (
(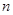 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前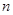 项和等于该数列的前
项和等于该数列的前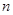 项之积,则称该数列为
项之积,则称该数列为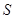 型数列。
型数列。
(1)若数列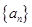 是首项
是首项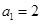 的
的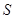 型数列,求
型数列,求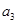 的值;
的值;
(2)证明:任何项数不小于3的递增的正整数列都不是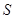 型数列;
型数列;
(3)若数列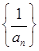 是
是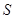 型数列,且
型数列,且 试求
试求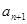 与
与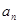 的递推关系,并证明
的递推关系,并证明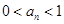 对
对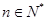 恒成立。
恒成立。
对于任意的 (
( 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前 项和等于该数列的前
项和等于该数列的前 项之积,则称该数列为
项之积,则称该数列为 型数列。
型数列。
(1)若数列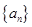 是首项
是首项 的
的 型数列,求
型数列,求 的值;
的值;
(2)证明:任何项数不小于3的递增的正整数列都不是 型数列;
型数列;
(3)若数列 是
是 型数列,且
型数列,且 试求
试求 与
与 的递推关系,并证明
的递推关系,并证明 对
对 恒成立。
恒成立。
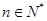 (
(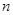 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前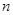 项和等于该数列的前
项和等于该数列的前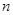 项之积,则称该数列为
项之积,则称该数列为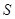 型数列。
型数列。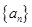 是首项
是首项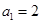 的
的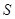 型数列,求
型数列,求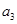 的值;
的值;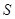 型数列;
型数列;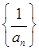 是
是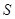 型数列,且
型数列,且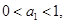 试求
试求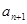 与
与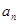 的递推关系,并证明
的递推关系,并证明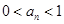 对
对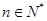 恒成立。
恒成立。 对于任意实数
对于任意实数 ,
, 和
和 恒成立。
恒成立。 的最大值为8,求b和c的值。
的最大值为8,求b和c的值。 在数列![]() 中,
中,![]() ,并且对于任意n
,并且对于任意n![]() ,且
,且![]() ,都有
,都有![]() 成立,令
成立,令![]()
(I)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前n项和
的前n项和![]() ,并证明:
,并证明:![]() <
<![]() 。
。
一、选择题:本大题共12个小题,每小题5分,共60分。
1―6BBCDBD 7―12CACAAC
二、填空题:本大题共4个小题,每小题4分,共16分。
13.0.8;
14.数学试题(理科).files/image155.gif)
15.数学试题(理科).files/image157.gif) ;
;
16.①③
三、解答题:
17.解:(1)由数学试题(理科).files/image159.gif) ,
,
得数学试题(理科).files/image161.gif)
数学试题(理科).files/image163.gif)
由正弦定得,得数学试题(理科).files/image165.gif)
数学试题(理科).files/image167.gif)
又B数学试题(理科).files/image169.gif)
数学试题(理科).files/image171.gif)
又数学试题(理科).files/image173.gif)
又数学试题(理科).files/image175.gif) 6分
6分
(2)数学试题(理科).files/image177.gif)
由已知数学试题(理科).files/image179.gif)
数学试题(理科).files/image181.gif) 9分
9分
当数学试题(理科).files/image183.gif)
因此,当数学试题(理科).files/image185.gif) 时,
时,
数学试题(理科).files/image187.gif)
当数学试题(理科).files/image189.gif) ,
,
数学试题(理科).files/image191.gif) 12分
12分
18.解:(1)依题意,甲答对主式题数数学试题(理科).files/image122.gif) 的可能取值为0,1,2,3,则
的可能取值为0,1,2,3,则
数学试题(理科).files/image194.gif)
数学试题(理科).files/image196.gif)
数学试题(理科).files/image198.gif)
数学试题(理科).files/image200.gif) 4分
4分
数学试题(理科).files/image202.gif) 的分布列为
的分布列为
数学试题(理科).files/image122.gif)
0
1
2
3
P
数学试题(理科).files/image204.gif)
数学试题(理科).files/image206.gif)
数学试题(理科).files/image208.gif)
数学试题(理科).files/image210.gif)
甲答对试题数数学试题(理科).files/image122.gif) 的数学期望为
的数学期望为
数学试题(理科).files/image212.gif) 6分
6分
(2)设甲、乙两人考试合格的事件分别为A、B,则
数学试题(理科).files/image214.gif)
数学试题(理科).files/image216.gif) 9分
9分
因为事件A、B相互独立,
数学试题(理科).files/image218.gif) 甲、乙两人考试均不合格的概率为
甲、乙两人考试均不合格的概率为
数学试题(理科).files/image220.gif)
数学试题(理科).files/image218.gif) 甲、乙两人至少有一人考试合格的概率为
甲、乙两人至少有一人考试合格的概率为
数学试题(理科).files/image222.gif)
答:甲、乙两人于少有一人考试合格的概率为数学试题(理科).files/image224.gif) 12分
12分
另解:甲、乙两人至少有一个考试合格的概率为
数学试题(理科).files/image226.gif)
答:甲、乙两人于少有一人考试合格的概率为数学试题(理科).files/image224.gif)
19.解法一(1)过点E作EG数学试题(理科).files/image228.gif) 交CF于G,
交CF于G,
|