
题目列表(包括答案和解析)
(本小题满分12分)二次函数![]() 的图象经过三点
的图象经过三点![]() .
.![]()
(1)求函数![]() 的解析式(2)求函数
的解析式(2)求函数![]() 在区间
在区间![]() 上的最大值和最小值
上的最大值和最小值
(本小题满分12分)已知等比数列{an}中,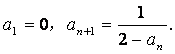
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设数列{an}的前n项和为Sn,证明:![]() ;
;
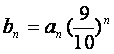 ,证明:对任意的正整数n、m,均有
,证明:对任意的正整数n、m,均有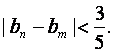
(本小题满分12分)已知函数![]() ,其中a为常数.
,其中a为常数.
(Ⅰ)若当![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
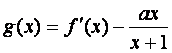 的单调区间.
的单调区间.(本小题满分12分)
甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为![]() ,乙投篮命中的概率为
,乙投篮命中的概率为![]()
(Ⅰ)求甲至多命中2个且乙至少命中2个的概率;
(Ⅱ)若规定每投篮一次命中得3分,未命中得-1分,求乙所得分数η的概率分布和数学期望.(本小题满分12分)已知![]() 是椭圆
是椭圆![]() 的两个焦点,O为坐标原点,点
的两个焦点,O为坐标原点,点![]() 在椭圆上,且
在椭圆上,且![]() ,圆O是以
,圆O是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与圆O相切,并且与椭圆交于不同的两点A、B.
与圆O相切,并且与椭圆交于不同的两点A、B.
(1)求椭圆的标准方程;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)当![]() 时,求弦长|AB|的取值范围.
时,求弦长|AB|的取值范围.
一、选择题:本大题共12小题,每小题5分,共60分。
CABD CDDC BABD
二、填空题:本大题共4小题,每小题4分,共16分。
13.3 14.1200 15..files\image234.gif) 16.
16..files\image236.gif)
三、解答题:本大题共6小题,共74分。
17.解:.files\image238.gif) 1分
1分
∵.files\image240.gif) ,∴
,∴.files\image242.gif) ⊥
⊥.files\image173.gif) ,∴∠
,∴∠.files\image244.gif)
在Rt△ADC中.files\image246.gif) 4分
4分
∴.files\image248.gif) 6分
6分
∵.files\image250.gif) 7分
7分
又∵.files\image252.gif) 9分
9分
∴.files\image254.gif)
.files\image256.gif) 12分
12分
18.解:(1)当.files\image185.gif) =7时,甲赢意味着“第七次甲赢,前6次赢5次,但根据规则,前5次中必输1次”,由规则,每次甲赢或乙赢的概率均为
=7时,甲赢意味着“第七次甲赢,前6次赢5次,但根据规则,前5次中必输1次”,由规则,每次甲赢或乙赢的概率均为.files\image259.gif) ,因此
,因此
.files\image261.gif) =
=.files\image263.gif) 4分
4分
(2)设游戏终止时骰子向上的点数是奇数出现的次数为.files\image016.gif) ,向上的点数是偶数出现的次数为n,则由
,向上的点数是偶数出现的次数为n,则由.files\image265.gif) ,可得:当
,可得:当.files\image267.gif)
.files\image269.gif) 或
或.files\image271.gif) ,
,.files\image273.gif) 时,
时,.files\image275.gif) 当
当.files\image277.gif) ,
,.files\image279.gif) 或
或.files\image281.gif) 因此
因此.files\image185.gif) 的可能取值是5、7、9 6分
的可能取值是5、7、9 6分
每次投掷甲赢得乙一个福娃与乙赢得甲一个福娃的可能性相同,其概率都是.files\image284.gif)
.files\image286.gif) 10分
10分
所以.files\image185.gif) 的分布列是:
的分布列是:
.files\image185.gif)
5
7
9
.files\image290.gif)
.files\image292.gif)
.files\image294.gif)
.files\image296.gif)
.files\image298.gif) 12分
12分
19.解:设数列.files\image154.gif) 的公比为
的公比为.files\image300.gif)
(1)若.files\image302.gif) ,则
,则.files\image304.gif)
显然.files\image190.gif) 不成等差数列,与题设条件矛盾,所以
不成等差数列,与题设条件矛盾,所以.files\image300.gif) ≠1 1分
≠1 1分
由.files\image190.gif) 成等差数列,得
成等差数列,得.files\image306.gif)
化简得.files\image308.gif) 4分
4分
∴.files\image310.gif) 5分
5分
(2)解法1:.files\image312.gif) 6分
6分
当.files\image018.gif) ≥2时,
≥2时,.files\image314.gif)
10分
.files\image316.gif)
.files\image318.gif)
.files\image320.gif)
=1+.files\image322.gif) 12分
12分
解法2:.files\image312.gif) 6分
6分
当.files\image018.gif) ≥2时,设
≥2时,设.files\image325.gif) 这里
这里.files\image327.gif) ,为待定常数。
,为待定常数。
则.files\image329.gif)
当n≥2时,易知数列.files\image331.gif) 为单调递增数列,所以
为单调递增数列,所以.files\image333.gif)
可见,n≥2时,.files\image335.gif)
于是,n≥2时,有.files\image337.gif) 10分
10分
.files\image316.gif)
.files\image339.gif)
=1+.files\image341.gif) 12分
12分
20.解法一:如图建立空间直角坐标系,
(1)有条件知.files\image343.gif) 1分
1分
由面.files\image200.gif) ⊥面ABC,AA1⊥A
⊥面ABC,AA1⊥A.files\image345.gif) 2分
2分
.files\image347.jpg)
.files\image349.gif)
∵.files\image351.gif) ……………3分
……………3分
∴.files\image353.gif) 与
与.files\image355.gif) 不垂直,即AA1与BC不垂直,
不垂直,即AA1与BC不垂直,
∴AA1与平面A1BC不垂直……5分
(2)由ACC
知.files\image357.gif) =
=.files\image353.gif) =
=.files\image359.gif) …7分
…7分
设平面BB.files\image361.gif) ,
,
由.files\image363.gif)
令.files\image365.gif) ,则
,则.files\image367.gif) 9分
9分
另外,平面ABC的法向量.files\image369.gif) (0,0,1) 10分
(0,0,1) 10分
.files\image371.gif)
所以侧面BB.files\image373.gif) 12分
12分
.files\image375.jpg) 解法二:(1)取AC中点D,连结A1D,则A1D⊥AC。
解法二:(1)取AC中点D,连结A1D,则A1D⊥AC。
又∵侧面ACC
∵A1D⊥面ABC ………2分
∴A1D⊥BC。
假设AA1与平面A1BC垂直,则A1D⊥BC。
又A1D⊥BC,由线面垂直的判定定理,
BC⊥面A
有两个直角,与三角形内角和定理矛盾。假设不
成立,所以AA1不与平面A1BC垂直………5分
(2)侧面BB
过点C作A
过点E作B
因为B
所以∠CFE即为所求侧面BB
由.files\image377.gif) 得
得.files\image379.gif)
在Rt△ABC中,cos∠.files\image381.gif)
所以,侧面BB.files\image373.gif) 12分
12分
21.(1)设.files\image214.gif) 与
与.files\image384.gif) 在公共点
在公共点.files\image386.gif) 处的切线相同。
处的切线相同。
.files\image388.gif) 。由题意知
。由题意知.files\image390.gif)
即.files\image392.gif) 2分
2分
解得.files\image394.gif) 或
或.files\image396.gif) (舍去,)
(舍去,).files\image398.gif)
.files\image400.gif) 4分
4分
.files\image402.gif)
.files\image404.gif) 可见
可见.files\image406.gif) 7分
7分
(2).files\image408.gif)
要使.files\image410.gif) 在(0,4)上单调,
在(0,4)上单调,
须.files\image412.gif) 在(0,4)上恒成立 8分
在(0,4)上恒成立 8分
.files\image414.gif) 在(0,4)上恒成立
在(0,4)上恒成立.files\image416.gif) 在(0,4)上恒成立。
在(0,4)上恒成立。
而.files\image418.gif) 且
且.files\image420.gif) 可为足够小的正数,必有
可为足够小的正数,必有.files\image422.gif) 9分
9分
.files\image424.gif) 在(0,4)上恒成立
在(0,4)上恒成立.files\image426.gif)
或.files\image428.gif) 11分
11分
综上,所求.files\image150.gif) 的取值范围为
的取值范围为.files\image430.gif) ,或
,或.files\image428.gif) ,或
,或.files\image422.gif) 12分
12分
.files\image434.jpg) 22.(1)∵点A的坐标为(
22.(1)∵点A的坐标为(.files\image436.gif) )
)
&
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com