|

0 1 2 



 。 。 17. 。提示:令 。提示:令 ,得 ,得 ;令 ;令 ,得 ,得 ;令 ;令 ,得 ,得 ;令 ;令 ,得 ,得 ;故 ;故 。 。 三、解答题 18.解:(I)    ――――7分 ――――7分
(II)因为 为锐角,且 为锐角,且 ,所以 ,所以 。――――9分 。――――9分     ――14分 ――14分
 19.解:(I)因为 19.解:(I)因为 平面 平面 , ,
所以平面 平面 平面 , , 又 ,所以 ,所以 平面 平面 , , 得 ,又 ,又 所以 平面 平面 ;――――4分 ;――――4分 (II)因为 ,所以四边形 ,所以四边形 为 为 菱形, 故 ,又 ,又 为 为 中点,知 中点,知 。 。 取 中点 中点 ,则 ,则 平面 平面 ,从而面 ,从而面 面 面 , , 过 作 作 于 于 ,则 ,则 面 面 , , 在 中, 中, ,故 ,故 , , 即 到平面 到平面 的距离为 的距离为 。――――9分 。――――9分 (III)过 作 作 于 于 ,连 ,连 ,则 ,则 , , 从而 为二面角 为二面角 的平面角, 的平面角, 在 中, 中, ,所以 ,所以 , , 在 中, 中, , ,  故二面角 故二面角 的大小为 的大小为 。14分 。14分
解法2:(I)如图,取 的中点 的中点 ,则 ,则 ,因为 ,因为 , , 所以 ,又 ,又 平面 平面 , , 以 为 为 轴建立空间坐标系, 轴建立空间坐标系, 则 , , , , , ,  , , , ,
 , , , ,
 ,由 ,由 ,知 ,知 , ,
又 ,从而 ,从而 平面 平面 ;――――4分 ;――――4分 (II)由  ,得 ,得 。 。 设平面 的法向量为 的法向量为 , , , , ,所以 ,所以  ,设 ,设 ,则 ,则
所以点 到平面 到平面 的距离 的距离  。――9分 。――9分 (III)再设平面 的法向量为 的法向量为 , , , , , , 所以  ,设 ,设 ,则 ,则 , ,
故  ,根据法向量的方向, ,根据法向量的方向, 可知二面角 的大小为 的大小为 。――――14分 。――――14分 20.解:(I)设 ,则 ,则 ,因为 ,因为 ,可得 ,可得 ;又由 ;又由 , , 可得点 的轨迹 的轨迹 的方程为 的方程为 。――――6分(没有 。――――6分(没有 扣1分) 扣1分) (II)假设存在直线 ,代入 ,代入 并整理得 并整理得  ,――――8分 ,――――8分
设 ,则 ,则  ――――10分 ――――10分 又   ,解得 ,解得 或 或 ――――13分 ――――13分
特别地,若 ,代入 ,代入 得, 得, ,此方程无解,即 ,此方程无解,即 。 。 综上, 的斜率的取值范围是 的斜率的取值范围是 或 或 。――――14分 。――――14分 21.解:(I) (1)当 时,函数 时,函数 是 是 增函数, 增函数, 此时, , ,  ,所以 ,所以 ;――2分 ;――2分
(2)当 时,函数 时,函数 是 是 减函数,此时, 减函数,此时, , ,  ,所以 ,所以 ;――――4分 ;――――4分
(3)当 时,若 时,若 ,则 ,则 ,有 ,有 ; ; 若 ,则 ,则 ,有 ,有 ; ; 因此, ,――――6分 ,――――6分 而 , , 故当 时, 时, ,有 ,有 ; ; 当 时, 时, ,有 ,有 ;――――8分 ;――――8分  综上所述: 综上所述: 。――――10分 。――――10分
(II)画出 的图象,如右图。――――12分 的图象,如右图。――――12分 数形结合,可得 。――――14分 。――――14分 22.解:
(Ⅰ)先用数学归纳法证明 , , . . (1)当n=1时,由已知得结论成立; (2)假设当n=k时,结论成立,即 .则当n=k+1时, .则当n=k+1时, 因为0<x<1时, ,所以f(x)在(0,1)上是增函数. ,所以f(x)在(0,1)上是增函数. 又f(x)在 上连续,所以f(0)<f( 上连续,所以f(0)<f( )<f(1),即0< )<f(1),即0< . . 故当n=k+1时,结论也成立. 即 对于一切正整数都成立.――――4分 对于一切正整数都成立.――――4分 又由 , 得 , 得 ,从而 ,从而 . . 综上可知 ――――6分 ――――6分 (Ⅱ)构造函数g(x)= -f(x)= -f(x)=  , 0<x<1, , 0<x<1, 由 ,知g(x)在(0,1)上增函数. ,知g(x)在(0,1)上增函数. 又g(x)在 上连续,所以g(x)>g(0)=0. 上连续,所以g(x)>g(0)=0. 因为 ,所以 ,所以 ,即 ,即 >0,从而 >0,从而 ――――10分 ――――10分 (Ⅲ)
因为  ,所以 ,所以 , ,  , , 所以 ――――① , ――――12分 ――――① , ――――12分 由(Ⅱ) 知: 知: , 所以 , 所以 = = , , 因为 , n≥2, , n≥2,  所以   < < < < = = ――――② . ――――14分 ――――② . ――――14分 由①② 两式可知:
 .――――16分 .――――16分
|

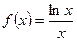 .
. 的单调性;
的单调性;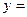
 +
+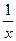 的图像总在直线
的图像总在直线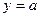 的上方,求实数
的上方,求实数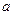 的取值范围;
的取值范围; 与
与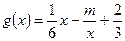 的图像有公共点,且在公共点处的切线相同,求实数
的图像有公共点,且在公共点处的切线相同,求实数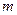 的值.
的值. (
(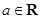 ).
). 的单调递减区间;
的单调递减区间; 时,若对
时,若对 有
有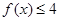 恒成立,求实数
恒成立,求实数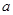 的取值范围.
的取值范围.![]() 在
在![]() 时取得极值,曲线
时取得极值,曲线![]() 在
在![]() 处的切线的斜率为
处的切线的斜率为![]() ;函数
;函数![]() ,
,![]() ,函数
,函数![]() 的导函数
的导函数![]() 的最小值为
的最小值为![]() .
.![]() 的解析式;
的解析式;![]() 的值;
的值;![]() .
. 是其左顶点,点C在椭圆上且
是其左顶点,点C在椭圆上且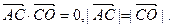
 和椭圆交于M,N两个不同点,求
和椭圆交于M,N两个不同点,求 面积的最大值,并求此时直线
面积的最大值,并求此时直线 的方程.
的方程.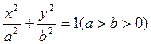 的离心率为
的离心率为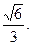
 的距离为
的距离为 求椭圆的方程;
求椭圆的方程;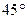 的直线
的直线 和椭圆交于A,B两点.
和椭圆交于A,B两点.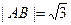 ,求b的值;
,求b的值; ,求实数
,求实数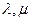 满足的关系式.
满足的关系式.