
题目列表(包括答案和解析)

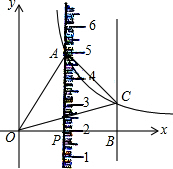 如图,平行于y轴的直尺(一部分)与双曲线y=
如图,平行于y轴的直尺(一部分)与双曲线y=| k | x |
如图1,点O是边长为1的等边△ABC内的任一点,设∠AOB= °,∠BOC=
°,∠BOC= °
°

(1)将△BOC绕点C沿顺时针方向旋转60°得△ADC,连结OD,如图2所示. 求证:OD=OC。

(2)在(1)的基础上,将△ABC绕点C沿顺时针方向旋转60°得△EAC,连结DE,如图3所示. 求证:OA=DE

(3)在(2)的基础上, 当 、
、 满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。
满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com