
题目列表(包括答案和解析)
直线![]() 过双曲线
过双曲线![]() 的右焦点,斜率k=2。 若
的右焦点,斜率k=2。 若![]() 与双曲线的两个交点分别在左 右两支上,则双曲线的离心率e的范围 ( )
与双曲线的两个交点分别在左 右两支上,则双曲线的离心率e的范围 ( )
A.e>![]() B.1<e<
B.1<e<![]() C.1<e<
C.1<e<![]() D.e>
D.e>![]()
在平面直角坐标系 中,曲线
中,曲线 与坐标轴的交点都在圆
与坐标轴的交点都在圆 上.
上.
(1)求圆 的方程;
的方程;
(2)若圆 与直线
与直线 交于
交于 、
、 两点,且
两点,且 ,求
,求 的值.
的值.
【解析】本试题主要是考查了直线与圆的位置关系的运用。
(1)曲线 与
与 轴的交点为(0,1),
轴的交点为(0,1),
与 轴的交点为(3+2
轴的交点为(3+2 ,0),(3-2
,0),(3-2 ,0) 故可设
,0) 故可设 的圆心为(3,t),则有32+(t-1)2=(2
的圆心为(3,t),则有32+(t-1)2=(2 )2+t2,解得t=1.
)2+t2,解得t=1.
(2)因为圆 与直线
与直线 交于
交于 、
、 两点,且
两点,且 。联立方程组得到结论。
。联立方程组得到结论。
下列命题:①过离心率为e且焦点在x轴,中心在原点的双曲线的右焦点F的直线与双曲线右支交于A、B两点,弦AB的垂直平分线交x轴于P,则![]() ;②若函数
;②若函数![]() ,则f(x)是周期函数;③如图,二面角
,则f(x)是周期函数;③如图,二面角![]() 的大小是45°,线段
的大小是45°,线段![]() .
.![]() ,
,
![]() 与
与![]() 所成的角为30°.则
所成的角为30°.则![]() 与平面
与平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() ;④三棱锥P—ABC的三条侧棱PA 、PB、PC两两垂直且长度均为1,四个顶点在同一个球面上,则A、B两点的球面距离是
;④三棱锥P—ABC的三条侧棱PA 、PB、PC两两垂直且长度均为1,四个顶点在同一个球面上,则A、B两点的球面距离是![]() ;其中正确的是 ;⑤已知
;其中正确的是 ;⑤已知![]() ,
,![]() ,且
,且![]() ,则
,则![]() 夹角的最大值是
夹角的最大值是![]() 。
。
给出下列命题:
①.在等差数列 中
中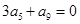 ,且
,且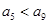 ,则使数列前n项和
,则使数列前n项和 取最小值的n等于5;
取最小值的n等于5;
② 的外接圆的圆心为O,半径为1,
的外接圆的圆心为O,半径为1, ,且
,且 ,则向量
,则向量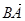 在向量
在向量 方向上的投影为
方向上的投影为 ;
;
③曲线 与直线
与直线 有两个交点,则
有两个交点,则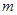 的取值范围是
的取值范围是 或
或 ;
;
④若定义在区间D上的函数f(x)对于D上任意n个值x1、x2、…xn总满足
 ,则f(x)称为D上的凸函数,现已知
,则f(x)称为D上的凸函数,现已知
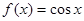 在
在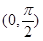 上凸函数,则锐角△ABC中
上凸函数,则锐角△ABC中 的最大值为
的最大值为 。
。
其中正确命题的序号是 。
给出下列命题:
①.在等差数列![]() 中
中![]() ,且
,且![]() ,则使数列前n项和
,则使数列前n项和![]() 取最小值的n等于5;
取最小值的n等于5;
②![]() 的外接圆的圆心为O,半径为1,
的外接圆的圆心为O,半径为1,![]() ,且
,且![]() ,则向量
,则向量![]() 在向量
在向量![]() 方向上的投影为
方向上的投影为![]() ;
;
③曲线![]() 与直线
与直线![]() 有两个交点,则
有两个交点,则![]() 的取值范围是
的取值范围是![]() 或
或![]() ;
;
④若定义在区间D上的函数f(x)对于D上任意n个值x1、x2、…xn总满足
![]() ,则f(x)称为D上的凸函
,则f(x)称为D上的凸函![]() 数,现已知
数,现已知![]() 在
在![]() 上凸函数,则锐角△ABC中
上凸函数,则锐角△ABC中![]() 的最大值为
的最大值为![]() 。 [来源:Zxxk.Com]
。 [来源:Zxxk.Com]
其中正确命题的序号是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com